Nächste Seite:
|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|
|
|
| Primzahlen | Lineare Algebra | Geometric Algebra | Clifford Algebra | Physik | Raumzeit | Quantenmechanik | Konstanten | Physiker | Farbenlehre |
| Prolog |
|
|
Ein Chemiker, ein Diplom Ingenieur, ein Bachelor of Science, ein Physiker und ein Mathematiker, haben die Aufgabe 2 mal 2 auszurechnen.
- Der Chemiker nimmt eine Tabelle, fährt auf dieser Tabelle mit dem Finger zwei Spalten nach rechts und zwei Zeilen nach unten und findet an dieser Stelle die Zahl 4.
- Der Ingenieur nimmt seinen Rechenschieber, bringt die beiden auf dem Rechenschieber aufgetragenen Zweien zur Deckung und peilt über den Daumen die Vier an.
- Der Bachelor of Science nimmt einen Taschenrechner tippt 2 mal 2 ein und bekommt als Resultat 3,99999999999999. Dieser Wert wird in voller Länge sorgfälltig auf einem Blatt Papier notiert.
- Der Physiker macht eine Reihenentwicklung, bricht diese nach dem zweiten Glied ab und bekommt als Resultat den Wert 3,8.
- Der Mathematiker macht auch eine Reihenentwicklung, kann aber keine Konvergenz feststellen, und kann deshalb das Problem nicht lösen.
| Überblick |
|
|
Weitere Mathematik Seiten
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Matrizen. Matrizen. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Mit einem Ada-Programm zum erzeugen großer Zahlen generierte Tabellen
Diese HTML-Seiten wurden vollständig mit einem Ada-Progamm erzeugt.
|
|
|
|
|
|
|
Weitere Links
Norman Wildberger's Kritik an der Logik der modernen Mathematik. |
Die ersten 100 000 Nachkommazahlen von PI |
| Matrizen |
|
|
Matrizen
Unter einer Matrix versteht man eine rechteckige Anordnung von Zahlen aij.
Eine Matrix ist vom Type (m, n) wenn sie m Zeilen und n Spalten hat.
Mann spricht dann auch von einer
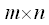 Matrix.
Matrix.
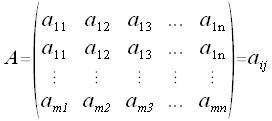
Eine Matrix ist Quadratisch wenn die Zahl der Zeilen gleich der Zahl der Spalten ist.
Also gilt: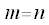
Für Matrizen kann man ähnlich wie für reelle oder komplexe Zahlen eine Addition und eine Multiplikation definieren.
Matrizen Addition
Eine Matrix Addition ist nur möglich, wenn die beiden zu addierenden Matizen die gleiche Anzahl von Zeilen und Spalten haben. Dies sei für die beiden Matrizen A und B der Fall. Dann kann man diese beiden Matrizen zu einer Matrix C addieren.
A + B = C.
Die einzelnen Elemente der Matrix C sind durch die Elemente von A und B wie folgt definiert:
aij + bij = cij
Matrizen Multiplikation
Bei der Produktbildung ist zu beachten, das eine Multiplikation von Matrizen in der Regel nicht kommutativ ist, also allgemein ist:
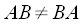 .
.
Will ich nun das Produkt C der beiden Matrizen A und B berechen, so ist desweiteren zu beachten, das die Anzahl der Spalten von A gleich der Anzahl der Zeilen von B ist. Das Matrizenprodukt der Matrizen A und B berechnet sich dann wie folgt:
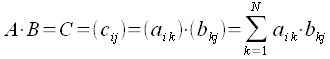
Transponierte Matrix
Die Transponierte einer Matrix, AT erhalte ich, in dem ich diese an der Diagonalen spiegele. Also die Zeilen und Spalten der Matrix A vertausche.
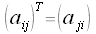
Beispiel:
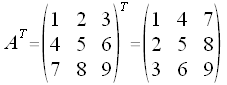
Kronecker Symbol
Das Kronecker Symbol ist wie folgt definiert.
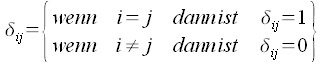
Kronecker Symbole werden in Formeln häufig zur Darstellung von Einheitsmatrizen verwendet.
Einheitsmatrix
Die Einheitsmatrix 1 (Manchmal auch mit E oder I bezeichnet) ist eine quadratische Matrix, in der alle Diagonalenelemente gleich Eins sind und die übrigen Matrixelemente gleich Null. Die Einheitsmatrix läßt sich durch das Kroneckersymbol definieren.
Beispiel: Eine 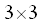 Einheitsmatrix:
Einheitsmatrix:
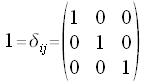
Wird eine Matrix mit der Einheitsmatrix multipliziert, so bleibt diese Matrix unverändert.
Reguläre Matrix
Wenn die Determinate einer quadratischen Matrix ungleich 0 ist, so bezeichnet man eine solche Matrix als eine reguläre Matrix.
Inverse Matrix
Sei A eine quadratische Matrix und sei die Determinate dieser Matrix ungleich null (reguläre Matrix), so existiert zu dieser Matrix eine Inverse Matrix.
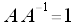
Wird eine Matrix mit der zugeordneten inversen Matrix multipliziert, so ist das Ergebnis eine Einheitsmatrix.
Damit wir die Inverse Matrix aus einer gegebenen Matrix berechnen können, benötigen wir die folgenden Definitionen:
Minore
Die Elemente der Minorenmatrix mij der Matrix A erhält man, wenn man aus der Matrix A die Zeile i und die Spalte j streicht und dann von der verbleibenden Matrix die Determinate bildet.
Cofaktoren (Kofaktoren)
Mit der Hilfe der Minoren einer Matrix lassen sich die Cofaktoren (Kofaktoren) definieren
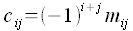
Berechnung der inversen Matrix
Die inverse Matrix läßt sich dann mit diesen Definitionen aus der Matrix A wie folgt berechnen.
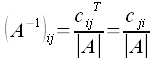
Dabei ist zu beachten, das bei der Cofaktoren-Matrix Zeilen und Spalten vertauscht sind. Also die Transponierte der Cofaktoren-Matrix, zu verwenden ist.
Weitere Informationen zu Matrizen findet man auf meiner Internetseite zum Thema Lineare Algebra.
| Vektorprodukte |
|
|
Kreuzprodukt (äußeres Produkt) von Vektoren (Vektorprodukt)
Im dreidimensionalen Fall wird durch das Vektorprodukt zweier Vektoren wieder ein Vektor erzeugt.
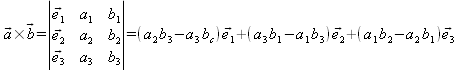
Mit dem Levi-Cita-Symbol schreibt sich das Kreuzprodukt als:
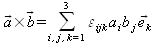
Der so erzeugte Vektor steht senkrecht auf der von den beiden Vektoren aufgespannten Ebene.
Der Betrag des Vektorproduktes gibt den Flächeninhalt des von 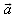 und
und
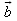 aufgespannten Parallelogramms an.
aufgespannten Parallelogramms an.
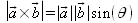
Dabei ist θ der Winkel zwischen den beiden Vektoren 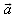 und
und
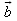 .
.
Der über das Vektorprodukt erzeugte Vektor lässt sich also wie folgt darstellen:
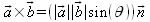
Dabei ist der Vektor 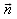 der zu
der zu
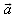 und
und
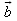 senkrechte Einheitsvektor.
senkrechte Einheitsvektor.
Kreuzprodukte im R n
Bisher haben wir nur Kreuzprodukte in R 3 betrachtet. Das Kreuzprodukt lässt sich auf beliebige Dimensionen des R n verallgemeinern. Bei n=3 war das Kreuzprodukt das Produkt von zwei Vektoren. Bei n=4 ist das Kreuzprodukt dann das Produkt von 3 Vektoren.
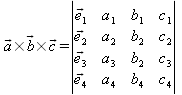
Allgemein wird im R n das Produkt von n-1 Vektoren gebildet.
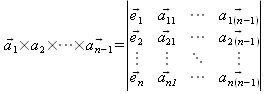
| Wichtige Matrizen in der Physik |
|
|
Wichtige Matrizen in der Physik
Metrischer Tensor in Galilei-Koordinaten
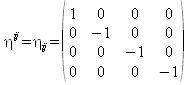
In dieser Form hat der metrische Tensor die Signatur ( 1, -1, -1, -1 ). In anderen Zusammenhängen findet man auch die Signatur (-1, 1, ,1, 1)
Pauli-Matrizen, Spin-Matrizen
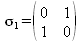
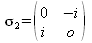
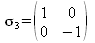
Einheitsmatrix 2x2
Beim Rechnen mit Spin-Matrizen ist oft die folgende (2x2) Einheitsmatrix hilfreich:
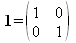
Algebra der Pauli Matrizen
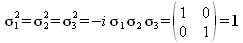
Pauli Matrizen und Quaternionen
Pauli-Matrizen bieten die Möglichkeit die Basis für einen Quaternionen Raum aufzubauen.
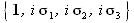
Auch über die folgenden Pauli-Matrizen lassen sich Quaternionen darstellen:
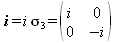
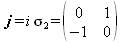
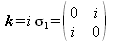
Die so definierten Matrizen haben die folgenden algebraischen Eigenschaften:
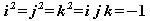
Dies entspricht der algebraischen Definition der Quaternionen.
Dirac-Matrizen - Gamma-Matrizen
Mit Hilfe der Pauli-Matrizen, lassen sich die diracschen Gamma-Matrizen wie folgt definieren:
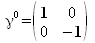
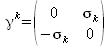 (k=1,2,3)
(k=1,2,3)
Setzt man die Paulimatrizen ein, so ergibt sich dann für die Gamma-Matrizen die folgende Form:

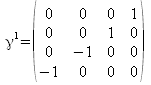
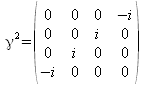
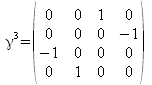
Man beachte, dass in der älteren Literatur die Matrix Gamma 0 auch häufig als Gamma 4 bezeichnet wird.
Algebra der Gamma-Matrizen
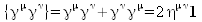
Kovariante Form der Gamma-Matrizen
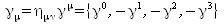
Mit Hilfe der vier oben definierten Gammamatrizen läßt sich eine weitere Matrix definieren, die in der Physik Anwendung findet. Diese wird als Gamma 5 bezeichnet.
| Affine Koordinaten |
|
|
Darstellung von Vektoren mit affinen Koordinaten
Darstellung von Vektoren mit Koordinaten eines schiefwinkligen Koordinatensystems
Verwendet man ein schiefwinkliges Koordinatensystem zu Darstellung eines Vektors so hat man zwei Möglichkeiten den Vektor in diesen Koordinatensystem darzustellen. Dies sind die kovariante- und die kontravariante Darstellung eines Vektors.
Bei kovarianten Koordinaten stehen die Indizes unten, bei kontravarianten Koordinaten stehen die Indizes oben. (Achtung! Nicht mit Potenzen verwechseln).
Kovariante Koordinaten:
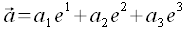
Kontravarinate Koordinaten:
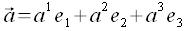
Im dreidimensionelen Raum besteht zwischen den kovarianten und den kontravarianten Basis-Vektoren die folgende Beziehung:
Es seien: 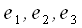 drei linear unabhängige Vektoren.
Diese können als Basis des dreidimensionalen Raumes verwendet werden.
Die dazu reziproken Basisvektoren werden wie folgt definiert:
drei linear unabhängige Vektoren.
Diese können als Basis des dreidimensionalen Raumes verwendet werden.
Die dazu reziproken Basisvektoren werden wie folgt definiert:
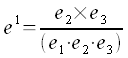
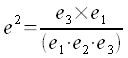
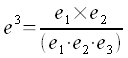
Unter 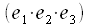 versteht man das Spatprodukt der drei Vektoren
versteht man das Spatprodukt der drei Vektoren 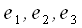 .
.
Weitere Zusammenhänge zwischen kovarianten- und kontravarianten Darstellugen von Vektoren
Es seien die affinen Koordinaten zweier Vektoren 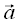 und
und
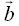 im Koordinatensystemen
im Koordinatensystemen
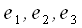 gegeben.
gegeben.
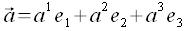
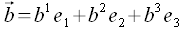
Die Koordinaten haben die kontravariante Form.
Mit der Hilfe des Skalarproduktes dieser beiden Vektoren lassen sich dann weitere Eigenschaften herleiten.
Berechnung des Skalarproduktes
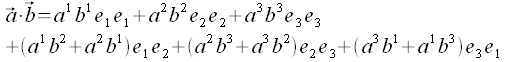
Die paarweisen Produkte der Koordinatenvektoren werden als metrischen Koeffizienten bezeichnet:
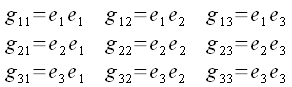
Die Matrix der metrischen Koeffizienten läßt sich dann wie folgt schreiben:

Das Skalarprodukt läßt sich mit Hilfe der Matrix
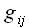 wie folgt darstellen:
wie folgt darstellen:
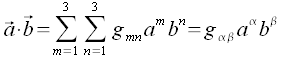
Beim letzten Term ist die Einsteinsche Summenkonvention gültig. Über die Indizes in griechischen Buchstaben wird von 1 bis 3 summiert, wenn diese jeweils einmal als oberere und unterer Indize auftreten.
Für kovariante Koordinaten lautet die Entsprechende Formel für das Scalarprodukt wie folgt:
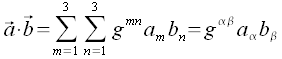
Wobei die 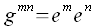 die metrischen Koeffizienten im System der reziproken Vektoren sind.
die metrischen Koeffizienten im System der reziproken Vektoren sind.
Diese hängen mit den Koeffizienten 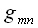 über die folgende Beziehung zusammen:
über die folgende Beziehung zusammen:

Dabei sind die 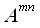 die Unterdeterminaten
der im Nenner stehenden Determinate die durch das wegstreichen der Zeile und Spalte entsteht in der sich das Element
die Unterdeterminaten
der im Nenner stehenden Determinate die durch das wegstreichen der Zeile und Spalte entsteht in der sich das Element
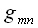 befindet entsteht.
befindet entsteht.
Ist der Vektor 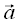 durch kovariante Koordinaten gegeben, der Vector
durch kovariante Koordinaten gegeben, der Vector 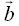 dagegen durch kontravariante Koordinaten, so ergibt sich das Skalarprodukt wie folgt:
dagegen durch kontravariante Koordinaten, so ergibt sich das Skalarprodukt wie folgt:
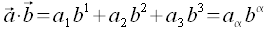
Ist die Form der Vektoren genau entgegengesetzt, so ergibt sich der folgende Zusammenhang für das Skalarprodukt:
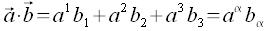
Damit ergeben sich dann die folgende Zusammenhänge:
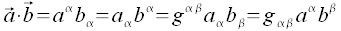
Daraus ergeben sich die folgenden Möglichkeiten der Umrechnung zwischen Kovarianter- und Kontravarianter Darstellung:
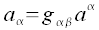
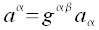
| Vektoranalysis |
|
|
Vektoranalysis
Am Anfang werden kartesische Koordinaten in drei Dimensionen angenommen. Die entsprechenen Aussagen werden dann in einem nächsten Schritt auf andere Koordinatensysteme verallgemeinert.
Nabla-Operator
Der Nabla-Differenzialoperator (Nabla-Operator) wird in kartesischen Koordinaten wie folgt definiert.
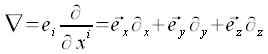
Der Nabla-Operator wird einerseits wie ein Vektor behandelt wirkt aber anderseits als Differenzialoperator, auf die rechts von ihm stehende Größe.
Anwendungen des Nabla-Operators
Mit der Hilfe des Nabla-Operators werde ich die Operationen Gradient, Divergenz und Rotation für kartesische Koordinaten definieren. Dabei wird der Nabla Operator auf ein scalares Feld Φ und ein Vektorfeld A angewendet. Da für Vektorfelder ein Äußeres- und ein Inneresprodukt definiert werden kann, lassen sich mit der Hilfe dieser Produkte und des Nabla Operators zwei Operationen definieren.
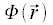
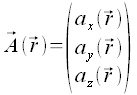
Gradient
Die Anwendung des Nabla-Operators auf ein scalares Feld ergibt ein Vektorfeld, dieses Vektorfeld wird als Gradient des Feldes bezeichnet. Dabei sind die Komponenten dieses Vektors, die partiellen Ableitungen des Feldes nach den einzelnen Koordinaten.
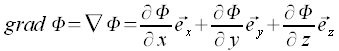
Divergenz
Das innere oder scalare Produkt des Nabla-Operators mit einem Vectorfeld ergibt ein scalares Feld, die Divergenz des Vectorfeldes.
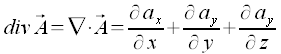
Rotation
Das äußere- oder Kreuzprodukt des Nabla-Operators mit einem Vektorfeld ergibt ein Vektorfeld, dieses Vektorfeld bezeichnet man als Rotation.
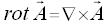
Die einzelnen Komponeten des Rotationsvektors lassen sich am übersichtlichsten über die folgende Determinante bestimmen.
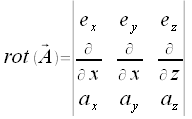
Mit dieser Determinate lassen sich die Komponeten des Vektors rot(A) wie folgt bestimmen:
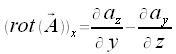
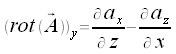
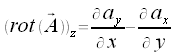
Formelsammlung - Anwendung des Napla-Operaturs auf die Produkte von Feldern
Durch die Anwendung des Nabla-Operators auf das Produkt von Feldern ergeben sich die folgenden Formeln
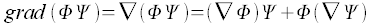
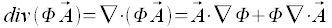
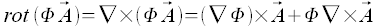
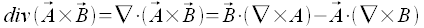
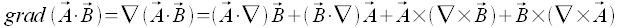
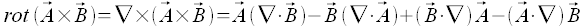
Mehrfache Anwendung des Nabla-Operators
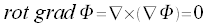
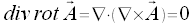
Laplace Operator
Der Laplace Operator ist in kartesischen Koordinaten wie folgt definiert:
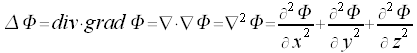
Für den Lapalace Operator gelten die folgenden Relationen:
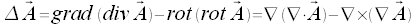
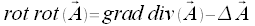
| Integralsätze |
|
|
Integralsätze
Gaußscher Satz
Der Gaußsche Satz gibt einen Zusammenhang zwischen der Divergenz eines Vektorfeldes innerhalb eines Volumens und dem Fluß des Vektorfeldes durch die Oberfläche F dieses Volumens an. Der Vektor dσ ist ein nach aussen gerichtetes Flächenelement der Oberfläche F die das Volumen V umgibt.
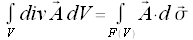
Stokesscher Satz
Der Stokessche Satz ermöglicht die Umwandlung eines Flächenintegrals in ein Kurvenintegral.
Im erten Integral wird über die Fläche F integriert. Im zweiten Integral, einem Kurvenintegral wir über den Rand R dieser Fläche integriert.
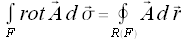
|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|
|
|
| Primzahlen | Lineare Algebra | Geometric Algebra | Clifford Algebra | Physik | Raumzeit | Quantenmechanik | Konstanten | Physiker | Farbenlehre |


 Meine Internetseite zum Thema Primzahlen.
Meine Internetseite zum Thema Primzahlen.






