|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|

|

|
| Physik | Raumzeit | Konstanten | Physiker | Physik-Links | Farbenlehre | Abkürzungen |
| Prolog |

|

|
Albert Einstein: "Der liebe Gott würfelt nicht!"
Einstein bekam 1921 den Nobelpreis für Physik, nicht für die Spezielle- und die Allgemeine-Relativitätstheorie, sondern für die Erklärung des photoelektrischen Effekts. Der photoelektrische Effekt zählt zu den grundlegenden Phänomenen der Quantenmechanik.
Obwohl Einstein, mit der Deutung des photoelektrischen Effektes, die Grundlagen der Quantenmechanik mitbegründet hatte, gehörte er Zeit seines Lebens, zu den Kritikern der Quantenmechanik. Er glaubte, dass die Quantenmechanik eines Tages durch eine fundamentalere Theorie abgelöst werden würde. Es war für ihn nicht akzeptabel, das der Zufall, die Grundgesetze der Natur regieren sollte.
Noch heute zählt die Vereinigung der beiden großen physikalischen Theorien, Quantenmechanik und Allgemeine Relativitätstheorie, zu den großen Herausforderungen der physikalischen Forschung.
Max Planck (1858-1947) deutscher Physiker Nobelpreis für Physik 1918.
Im Jahre 1900 gab Max Planck bekannt, er habe unter einigen etwas merkwürdigen Annahmen eine Verteilungsfunktion für die Schwarzkörperstrahlung herleiten können. Die Verteilungsfunktion der Schwarzkörperstrahlung war damals durch Messungen bekannt. Es war damals aber nicht möglich, aus den damals bekannten physikalischen Theorien, die Verteilungsfunktion der Schwarzkörperstrahlung herzuleiten.
Max Planck nahm, in seiner Herleitung der Schwarzkörperstrahlung an, das die elektromagnetische Strahlung in diskreten Energiepaketen E, in Abhänigkeit von der Frequenz v, gequantelt ist. Das heißt die Werte der Energien die den einzelnen diskreten Energiepaketen den Quanten zugeordnet werden, berechnen sich in der Abhängigkeit von der Frequenz nach der folgenden Gleichungen:
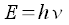
Der Wert h = 6,626076 * 10-34 Js ist die Plancksche Konstante (Wirkungsquantum).
Max Planck: "Ich kann die ganze Prozedur als einen Akt der Verzweiflung charakterisieren, da ich von Natur aus friedlich bin und alle zweifelhaften Abenteuer ablehne."
Die Quantenhypothese, welche durch diese Gleichung impleziert wurde, war Planck und anderen Physikern suspekt und vor 1905 nicht allgemein anerkannt.
Dann aber verwendete Einstein die gleiche Idee zur Erklärung des photoelektrischen Effektes. Die Quantelung der elektromagnetischen Strahlung in diskrete Energiepakete E = hv, ist eine fundamentale Eigenschaft der elektormagnetischen Strahlung.
Louise de Broglie französischer Physiker (1892-1987). Nobelpreis für Physik 1926:
"Nach dem Ersten Weltkrieg dachte ich viel über die Quantentheorie und den Welle-Teilchen-Dualismus nach... Plötzlich hatte ich eine Eingebung:
Der von Einstein postulierte Welle-Teilchen-Dualismus, für elektromagnetische Wellen, mußte ein absolut allgemeines, der gesamten physikalischen Natur innewohnendes Phänomen sein, welcher auch für andere Elementarteilchen gilt."
Erwin Schrödinger österreichischer Physiker(1887-1961). Nobelpreis für Physik 1933
Im November 1925 hielt Erwin Schrödinger in Zürich ein Seminar zu de Broglies Arbeit ab. Dabei wurde er gefragt: "Sie sprechen über Wellen, aber wo ist die Wellengleichung?". Daraufhin entwickelte Schrödinger die nach ihm benannte Gleichung und stieß damit das Tor zu einer neuen Physik auf.
Ungefähr zur gleichen Zeit lieferten Max Born, Pascual Jordan und Werner Heisenberg eine zur Schrödigner-Gleichung äquivalente Formulierung der Quantenmechanik mittels Matritzen.
Die Äquivalenz der Darstellung der Quantenmechanik mittels der Matrizenmechanik oder der Schrödinger-Gleichung wurde von Wolfgang Pauli gezeigt.
Schrödingers Katze lebt!
Richard P. Feynman amerikanischer Physiker (1918-1988). Nobelpreis für Physik 1965:
"Ich las in einer Zeitung, es soll eine Zeit gegeben haben, in der nur 12 Leute Albert Einsteins Relativitätstheorie verstanden. Ich glaube nicht, dass es jemals eine solche Zeit gab, aber ich kann mit Sicherheit sagen, daß niemand die Quantenmechanik versteht."
| Einleitung |

|

|
Viele physikalische Phänomene lassen sich nicht durch die Modelle der "klassischen" Physik, wie der klassischen Mechanik, Elektrodynamik und Thermodynamik, verstehen. Um diese Phänomene zu beschreiben, sind andere Theorien und Modelle erforderlich als in der klassischen Physik.
Beispiele:
- Atomphysik:
Diskretes Spektrum der emittierten und absorbierten elektromagnetischen Strahlung. Größe und Stabilität der Atome. - Kernphysik
Größe und Stabilität der Atomkerne, Alphazerfall, Spaltung, Fusion - Chemie
Struktur der chemischen Bindung, Form und Größe von Molekülen, chemische Reaktionen. - Festkörperphysik
Mechanische, thermische, elektrische und magnetische Eigenschaften, zum Beispiel die spezifische Wärme bei tiefen Temperaturen oder die Supraleitung. - Makroskopische Quantenphänomene
Supraleitung, Suprafüssigkeit, Hohlraumstrahlung.
Oft beziehen sich quantenmechanische Effekte auf den mikroskopischen Bereich, die klassische Physik dagegen auf makroskopische Bereiche. Viele makroskopische Phänomene, sind aber nur quantenmechanisch zu verstehen.
| Gleichungen der Quantenmechanik |

|

|
Die Schrödinger-Gleichung und die Klein-Gordon-Gleichung sind die grundlegenden Gleichungen der Quantenmechanik. Dies sind Wellengleichungen, die analog zu klassischen Wellengleichungen entwickelt wurden.
Diese Gleichungen lassen sich aber nicht aus der klassischen Physik herleiten. Deshalb sind diese Gleichungen, die Axiome der Quantenmechanik. Dass diese Gleichungen richtig sind, kann nur durch Experimente überprüft werden. Alle, bisher durchgeführten Experimente, haben aber die Aussagen der Quantenmechanik bestätigt.
Kann man eine dieser Gleichungen, für ein bestimmtes Quantenmechanisches System aufstellen und lösen, so beinhalten diese Lösungen alle Informationen, die man über dieses quantenmechanisches System gewinnen kann.
Die Lösungen dieser Gleichungen sind sogenannte Wellenfunktionen. Diese Wellenfunktionen symbolisieren den Wellencharacter der Elementarteilchen. Eine Wellenfunktion hat complexe Funktionswerte, und hat keine direkte physikalische Bedeutung.
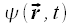
Erst durch das durchführen, bestimmter mathematischer Operationen, auf die Wellenfunktion, können physikalische Informationen über das System berechnet werden.
Beispiel:
Hat man eine Wellenfunktion, welche das Verhalten eines Teilchens in einem System beschreibt,
so kann man, durch die folgende mathematische Operation, die Aufenthaltswahrscheinlichkeit des Teilchens in einem
kleinen Volumen berechnen.
Man multipliziert das Betragsquadrat der Wellenfunktion mit einem kleinen Volumen dv (Das Betragsquadrat der Wellenfunktion sollte sich in diesem kleinen Volumen nicht nennenswert ändern).
Der erhaltene Zahlenwert ist ein Maß für die Wahrscheinlichkeit, das Teilchen in diesem Volumen zu finden.
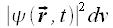
Das Betragsquadrat der Wellenfunktion ist also eine Wahrscheinlichkeitsdichtefunktion, mit der Einheit 1/Volumen.
Da man das Teilchen finden muß, wenn man den gesamten Raum absucht, ist es sinnvoll die Wellenfunktion so zu normieren, das sich der Wert 1 ergibt, wenn man über den ganzen Raum integriert.
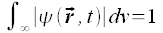
Integriert man nur über ein Volumen V1, so bekommt man die Wahrscheinlichkeit dafür,
das Teilchen im Volumen V1 zu finden. Dies gilt für beliebige Volumina.
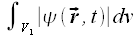
Die Schrödinger-Gleichung ist die Grundgleichung der nichtrelativistischen Quantenmechanik:
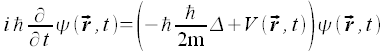
Die Klein-Gordon-Gleichung ist die Grundgleichung der relativistischen Quantenmechanik:
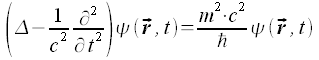
Die Dirac-Gleichung ist die Grundgleichung für die quantenmechanische Beschreibung des Elektrons und des Positrons.
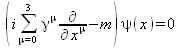

|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|

|

|
| Physik | Raumzeit | Konstanten | Physiker | Physik-Links | Farbenlehre | Abkürzungen |