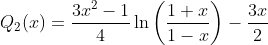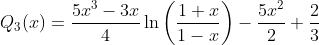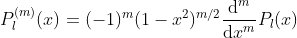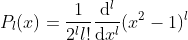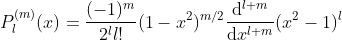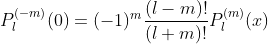Mathematical Functions - Legendre Polynomials
Definition of the Legendre polynomial Pn(x).
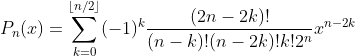
Even or odd Legendre polynomials.
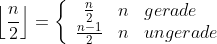
Rodrigues formular for Legendre polynomials.
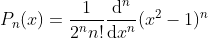
The Legendre polynomials are solutions of the Legendre differential equation.
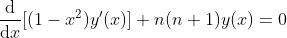
Executing the derivative d/dx will result in the following differential equation:
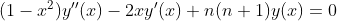


 English
English