Primzahlenfakultät - Primorial

Es gibt den Begriff der Fakultät einer natürlichen Zahl n!. Verwendet man anstelle der natürlichen Zahlen Primzahlen so findet man die Begriffe: Primzahlenfakultät, Primorial und Primfakultät. Da diese Begriffe immerwieder etwas anders definiert sind, verwende ich diese wie folgt:

- Primorial <=> Primzahlenfakultät (Premorial first definition).

- Primfakultät (Primorial second definition).

Siehe auch genaue Definitionen weiter unten.

Primzahlenfakultät - Primorial I

Die Primzahlenfakultät wird auch als Primorial bezeichnet.

Englische Bezeichnung

Die Folge der Primzahlfakultäten hat die OEIS Nummer A002110 und hat dort den Namen: "Primorial numbers (first definition)".

Die Abkürzung OEIS steht für "The On-Line Encyclopedia of Integer Sequences - OEIS".

Definition und Bezeichnung

Die Primzahlenfakultät P_n# ist das Produkt der ersten Primzahlen P_i von 2 bis P_n bzw. i von 1 bis n.

P_n# = 2⋅3⋅...⋅P_n;

Tabelle der Primzahlenfakultäten

Relation zur Eulerschen Zahl e

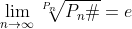
Durch Logarithmieren ergibt sich das folgende asymptotische Verhalten:

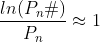
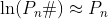
Euklidische Zahlen

Die Primzahlenfakultät steht in engem Zusammenhang mit den Euklidischen Zahlen E_n.

E_n=P_n#+1;

Eine Tabelle der ersten 100 Euklidischen Zahlen findet man hier:

Euklidische Zahlen

Kummer-Zahl

K_n=P_n#-1;

Die Kummer-Zahl wir auch als Euklidische Zahl der zweiten Art bezeichnet.

Primfakultät - Primorial II

Die Primfakultät ist die Folge A034386 in der OEIS. Diese Folge hat dort den Namen: "Primorial numbers (second definition)".

Definition und Bezeichnung

Die Primfakultät n# einer natürlichen Zahl n ist das Produkt aller Primzahlen kleiner oder gleich n.

n# = 2⋅3⋅...⋅P_k mit P_k≤n;

Da die kleinste Primzahl die 2 ist, man die Primfakultät n# aber auch für die Werte 0# und 1# definieren möchte, ist es Konvention 0#=1 zu setzen und für 1#=1 zu verwenden.

n	0	1	2	3	4	5	6	7	8	9	10	11	12	13
n#	1	1	2	6	6	30	30	210	210	210	210	2310	2310	30030

Tschebyschew θ-Funktion

Tchebyschew's θ-Funktion ist der Logarithmus der Primfakultät.

θ(n) = ln(n#)

Durch den Logarithmus kann das Produkt durch eine Summe ersetzt werden.

Die Primzahlenfakultät und Verteilungsmuster der Primzahlen in den natürlichen Zahlen

Primzahlenfakultät P_n# als Zeilenlänge

Um Muster in der Primzahlen in den natürlichen Zahlen zu finden kann man die natürlichen Zahlen in rechteckigen Schemata anordnen und die Primzahlen markieren. Nimmt man die Primzahlenfakultät als Zeilenlänge, so ergeben sich die folgenden Muster der der Primzahlen innerhalb der natürlichen Zahlen.

Primzahlenfakultät P₁# = 2

Tabelle mit Zeilenlänge = 2

Primzahlenfakultät P₂# = 6

Tabelle mit Zeilenlänge = 6

Dies Tabelle spielt eine wichtige Rolle beim Auffinden von Primzahlen-Zwillingen.

Tabelle P₂#=6

Primzahlenfakultät P₃# = 30

Tabelle mit Zeilenlänge = 30

Eine größere Tabelle mit einer Zeilenlänge von 30 findet man auf einer seperaten Seite.

Tabelle P₃#=30

Primzahlenfakultät P₄# = 210

Die Tabelle mit einer Zeilenlänge von 210 findet man auf einer seperaten Seite.

Tabelle P₄#=210

Primzahlenfakultät P₅# = 2310

Die Tabelle mit einer Zeilenlänge von 2310 findet man auf einer seperaten Seite.

Tabelle P₅#=2310

Division mit Rest

Für positive Zahlen gilt:

a = m*b + r

a, b, m, r ∈ ℕ₀ und b ≠ 0;

Modulo

a mod b = r; wenn a und b positiv sind.

Modulare Arithmetik (Gauß)

Wenn gilt a mod b = r so sind dazu die folgenden Aussagen äquivalent:

⇔ Wenn a und r durch b geteilt werden, so bleibt in beiden Fällen der gleiche Rest.

⇔ a-r ist durch b teilbar.

⇔ b|(a-r); b teilt (a-r).

Beispiel:

7 mod 5 = 2;

7/2 = 3 Rest 1; 5/2 = 2 Rest 1.

(7-5) = 2; 2/2 = 1 Rest 0.

2|(7-5) = 2|2; 2 teilt 2.

Dirichletscher Primzahlsatz

Teilerfremd

Zwei natürliche Zahlen sind teilerfremd, wenn sie keinen gemeinsamen Primfaktor haben. Im englischen werden die Begriffe relative prime oder auch coprime verwendet

Dirichletscher Primzahlsatz

Sind die natülichen Zahlen a,b teilerfremd. So enthält die Folge a+i⋅b undendlich viele Primzahlen. (Dabei ist i eine positive ganze Zahl).

a, a+b, a+2b, a+3b, ...

Koordinaten der natürlichen Zahlen

Hat man die natürlichen Zahlen in einer Matrix oder in einem rechteckigen Schema angeordnet, so dass jede Zahl sich in einer bestimmten Zeile und in einer bestimmten Spalte dieses Schemas befindet, so kann man den natürlichen Zahlen in diesem Schema, Koordinaten in der Form der Spaltennummer und der Zeilennummer zuordnen.

Wählt man als Zeilenlänge die Primzahlenfakultät P_n# und ordnet die natürlichen Zahlen beginnend mit 1 in aufsteigender Reihenfolge an, so kann man eine natürliche Zahl n∈ℕ wie folgt mit der Primzahlenfakultät P_k#, dem Zeilenindex i und dem Spaltenindex j parametrisieren:

n = i·P_k#+j;

mit j,k∈ℕ und i ist eine nicht negative ganze Zahl i∈ℕ₀.

Der Wert j ist der Spaltenindex und läuf von 1 bis P_k#.

Der Wert i beginnt mit dem Wert 0 und läuf bis zum Anzahl der Zeilen minus 1. Dadurch hat i in der ersten Zeile den Wert 0. In der ersten Zeile ist also n=j.

Allgemeine Beobachtungen zur Primzahlenfakultät P_n# als Zeilenlänge

Die natürlichen Zahlen werden in einem rechteckigen Schema angeordnet. Wenn man als Zeilenlänge die Primzahlenfakultät P_n# nimmt, so stehen die Primzahlen unterhalb der ersten Zeile, nur in bestimmten Spalten. In einer solchen Anordnung der natürlichen Zahlen, lassen sich bestimmte Gesetzmäßigkeiten ablesen und dann mit Hilfe des Dirichletschen Primzahlsatzes beweisen. Die Primzahlenfakultät P_n# dient als Ordungselement, welches bestimmte Gesetzmäßigkeiten sichtbar macht.

Beispiel

Anordnung der natürlichen Zahlen, in einem rechteckem Schema mit der Primzahlenfaklultät P₃#=30= 2⋅3⋅5 als Zeilenlänge.

Besondere Rolle der ersten Zeile

Die Zahlen in der ersten Zeile dienen der Nummerierung der entsprechenden Spalten.

In der ersten Zeile stehen die natürlichen Zahlen von 1 bis zur Primzahlenfakultät P_n#.

Muster die unterhalb der ersten Zeile auftreten, werden von der Primzahlenverteilung in der ersten Zeile und der Primzahlenfakultät P_n#, dem letzten Element der ersten Zeile bestimmt.

Wo findet man die Primzahlen?

Unterhalb der ersten Zeil, treten Primzahlen nur in bestimmten Spalten auf.

Kenne ich also die erste Zeile, so ist durch diese Festgelegt, in welchen Spalten Primzahlen auftreten können.

Primzahlen in den Spalten 1 bis P_n

In den Spalten von 1 bis P_n treten Primzahlen nur in der ersten Zeile und in der ersten Spalte unterhalb der 1 auf.

Primzahlen in der ersten Spalte

Die Zahlen in der ersten Spalte haben ab der zweiten Zeile die Struktur: P_n#+1.
P_n#+1 ist Teilerfremd mit P_n#.

Folglich enthält die Folge (P_n#+1) + i⋅P_n# unendlich viele Primzahlen (Dirichletscher Primzahlsatz).

Primzahlen in Spalten zwischen P_n und P_n#

Speziell gilt für P₂#=6 und P₃#=30:

Im Bereicht zwischen P_n und P_n# treten Primzahlen nur in Spalten auf, in denen in der ersten Zeile eine Primzahl steht.
Die übrigen Spalten, bei denen in der ersten Zeile keine Primzahl steht sind, Primzahlen frei.

Eine Primzahl P_a die wischen P_n und P_n# liegt, für die also gilt P_n<P_a<P_n#, ist teilerfremd zu P_n#, da P_n# nur aus Primfaktoren besteht, die kleiner oder gleich P_n sind.

Folglich enthällt die Folge P_a+i⋅P_n#, welche die Zahlen der Spalte P_a bildet, unendlich viele Primzahlen (Dirichletscher Primzahlsatz).

Allgemein können in der ersten Zeile auch Produkte von Primzahlen P_a auftreten, für die gilt P_n<P_a<P_n#.
Diese sind natürlich auch teilerfremd zu P_n#.
Folglich können in diesen Spalten auch beliebig viele Primzahlen auftreten.

Primzahlen freie Bereiche

Die Spalten innerhalb des Bereichs von 1 bis P_n+1 sind unterhalb der ersten Zeile Primzahlen frei.

Speziell gilt für P₂#=6 und P₃#=30:
Ist eine Zahl der ersten Zeile keine Primzahl, so ist die gesamte Spalte Primzahlen frei.

Zusammengesetzte Zahlen in Spalten mit Primzahlen

Zahlen die keine Primzahlen sind und in Spalten auftreten die Primzahlen enthalten, sind Produkte von Primzahlen, die größer sind als der größte Faktor P_n der verwendeten Primzahlenfakultät P_n# (siehe Beispiel 1 und Beispiel 2).

Beispiel 1

In der unteren Tabelle der Natürlichen Zahlen mit P₂=3 und der Primzahlenfakultät P₂#=6=2⋅3, als Zeilenlänge, findet Primzahlen man nur in der ersten und in der fünften Spalte.

Die zusammengesetzten Zahlen 25=5*5 und 35=5*7 sind Produkte der Primzahlen 5 und 7.

Die Primzahlen 5 und 7 sind beide grösser als P₂ = 3. Diese findet man in Spalten mit Primzahlen.

Beispiel 2

Tabelle der Natürlichen Zahlen mit P₃=5 und der Zeilenlänge P₃#=30.

Nächste Seite - Next Page Prime Twins:

Primzahlen-Zwillinge