Gamma Function - Γ(z)
The Gamma Function - Γ(z) was developed by Leonhard Euler to generalise the factorial n! to non-integer values.
The following relation between the factorial and the gamma function with integer arguments is given:
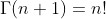
Definiton
The first definition of the gamma function was given by Euler in 1730 in a letter to Goldbach.
For x > 0 we have:
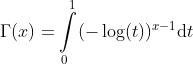
or in the following equivalent form:
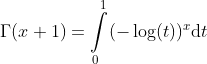
By a change of variables the integral becomes the following form:
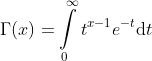
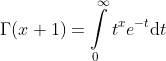
Alternative Definition
The gamma function can be defined by using the following product:
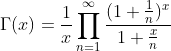
Relation to the Mellin Transformation
The gamma function Γ(x) is a special case of a Mellin Transformation Mf (x):
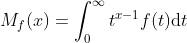
The gamma function Γ(x) is the Mellin transform of f(t) = e-t.
Properties
For integer values we have:
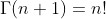
As generell formular we have:
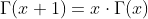
Negative Values
Rearranging the above formular will give:
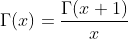
The right side of this expression is defined for negative x in the range between -1 > x > 0.
Using the value -1/2 as value for x in this formular we get:
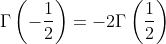
For other negative values of x with x+n>0, except negative integers and zero (0, -1, -2, -3, ...) we can generalise the formular above:
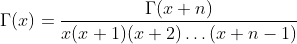
Derivatives
First derivative of the gamma function:
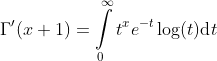
N'th derivatives of the gamma function:
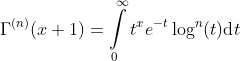
Relation between the Riemann zeta function and the gamma function
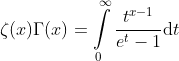
Further Relations
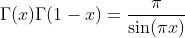
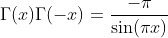
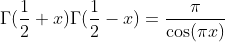
Special Values
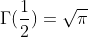


 English
English



