
|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|

|

|
| Physik | Mechanik | Elektrodynamik | Quantenmechanik | Konstanten | Physiker | Physik-Links | Farbenlehre | Abkürzungen | Mathematik |
| Prolog |

|

|
Hermann Minkowsky, 80. Versammlung Deutscher Naturforscher und Ärzte 1908 in Köln:
"Die Anschauungen über Raum und Zeit, die ich Ihnen entwickeln möchte, sind auf experimentell-physikalischem Boden erwachsen. Darin liegt ihre Stärke. Ihre Tendenz ist eine Radikale. Von Stund an sollen Raum für sich und Zeit für sich völlig zu Schatten herabsinken, und nur noch eine Art Union der beiden soll Selbstständigkeiten bewahren."
| Die kürzeste Geschichte der Raumzeit |

|

|
Grundlegende Gleichungen zur Beschreibung der Struktur von Raum und Zeit:
| Pythagoras | s2 | = | x2 + y2 |
| Euklid | s2 | = | x2 + y2 + z2 |
| Albert Einstein "Spezielle Relativitätstheorie" | s2 | = | c2t2 - (x2 + y2 + z2) |
| Albert Einstein "Allgemeine Relativitätstheorie" | ds2 | = | c2dt2 - (dx2 + dy2 + dz2) |
Definitionen
| c | : | Lichtgeschwindigkeit |
| t | : | Zeit; |
| x, y, z | : | Seitenlängen in kartesische Koordinaten |
| s | : | Abstand zwischen zwei Punkten |
| d | : | kennzeichnet eine infinitismal kleinen Wert. |
| Der Satz des Pythagoras |

|

|
s2 = x2 + y2
s ist der Abstand zwischen zwei Punkten auf der Ebene.
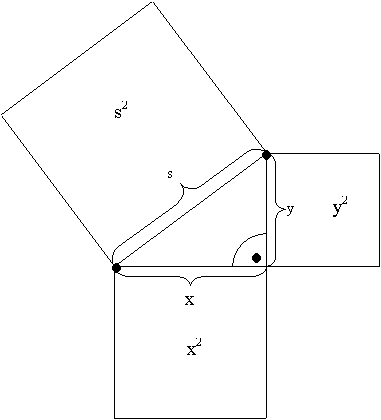
Der Satz des Pythagoras beschreibt die Abhängigkeiten der Seitenlängen eines rechtwinkligen Dreieckes.
"In einem rechtwinkligen Dreieck ist die Fläche des Quadrates über der Hypotenuse gleich der Summe der Flächen der beiden Kathetenquadrate."
Der Satz des Pythagoras wurde lange dem griechischen Philosophen Pythagoras (ca. 580-500 v.Chr) zugeschreiben. Neuere Archeologische Erkentnisse weisen aber darauf hin, das schon die Babylonier zwischen 1800 - 1650 v.Chr den "Satz des Pythagoras" anwendeten. Das wissen um diese geometrischen Zusammenhänge ist also älter als Phythagoras.
| Der euklidische Raum |

|

|
Die Verallgemeinerung, des Satzes des Pythagoras auf drei Dimensionen, kann im allgemeinen wie folgt geschreiben werden:
s2 = x2 + y2 + z2
s ist der Abstand zwischen zwei Punkten im Raum. Diese Verallgemeinerung, des Satzes des Pythagorases, stellte die fundamentale Struktur des Euklidschenraumes dar.
Vor Einstein herrschte die Auffassung, das die mathematische Struktur des euklidischen Raumes, der physikalischen Struktur des Raumes entspricht.
Aber bereits der große Mathematiker Carl Friedrich Gauß machte sich, aus Anlaß von konkreten Messungen, Gedanken darüber ob dies die wahre Struktur des Raumes ist.
Er ließ deshalb Georg Friedrich Bernhard Riemann über dieses Thema arbeiteten. Die Ergebnisse dieser mathematischen Arbeit wurde am 10. Juni 1854 in der Vorlesung "Über die Hypothesen, welche der Geometrie zugrunde liegen", der wissenschaftlichen Öffentlichkeit vorgestellt. Von da an war die mathematische Möglichkeit eines nicht euklidischen Raumes der wissenschaftliche Öffentlichkeit bekannt.
Insbesondere wies Riemann in seinem Vortrag darauf hin, daß die wahre Struktur des physikalischen Raumes nur durch Messungen bestimmt werden kann und nicht durch das Studium der 2000 Jahre alten Bücher des Euklid.
Es blieb Albert Einstein überlassen, die mathematische Beschreibung des realen physikalischen Raumes mit seiner speziellen und allgemeinen Relativitätstheorie weiter zu entwickeln.
| Albert Einstein "Spezielle Relativitätstheorie" |

|

|
Axiome der Speziellen Relativitätstheorie
Die Spezielle Relativitätstheorie beruht auf den folgenden Axiomen:
- Die Lichtgeschwindigkeit ist in allen Inertialsystemen gleich.
- Die Naturgesetze sind in allen Inertialsystemen gleich.
Inertialsysteme, sind Bezugsysteme, die sich mit konstanter Geschwindigkeit, relativ zueinander bewegen. Beschleunigte Bezugssysteme sind keine Inertialsysteme. Insbesondere sind sich drehende Bezugssysteme keine Inertialsysteme. Desweiteren sind Inertialsysteme dadurch gekennzeichnet, das in Ihnen das Newtonsche Trägheitsgesetz gilt. Die Newtoschen Axiome gelten nicht in beschleunigten Systemen.
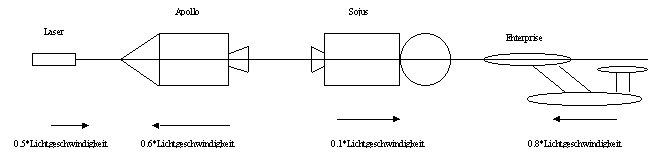
Die Gleichheit der Lichtgeschwindigkeit in allen Inertialsystemen habe ich in dem oberen Bild versucht zu veranschaulichen:
- Ein Laser sendet einen Laserlichtstrahl aus.
- Dieser durchläuft drei Raumschiffe: Apollo, Sojus und die Enterprise.
- Jedes dieser drei Raumschiffe kann die Geschwindigkeit des Laserlichtes messen.
- Jedes dieser drei Raumschiffe und der Laser bewegen sich mit einer anderen Geschwindigkeit relativ zum Bildrahmen.
Dabei wird es, bei der Messung der Lichtgeschwindigkeit in den drei Raumschiffen, zu dem folgenden Ergebnis kommen:
- Jedes dieser drei Raumschiffe wird die gleiche Geschwindigkeit des Lichtstrahls messen, unabhängig von der Geschwindigkeit der drei Raumschiffe oder des Lasers, der den Lichtstrahl aussendet.
Diese Eigenschaft unseres Universums ist es, aus der die anderen seltsamen Eigenschaften der speziellen Relativitätstheorie abgeleitet werden.
Die Tatsache, daß die Lichtgeschwindigkeit in allen Bezugssystemen gleich ist, wurde zum ersten Mal durch die Messungen von Michelson-Morley entdeckt. (Bei diesem Versuch wollte man die Geschwindigkeit der Erde relative zum absoluten Raum bzw. dem Äther bestimmen. Es zeigte sich aber, daß sich das Licht in alle Richtungen mit der gleichen, konstanten Geschwindigkeit ausbreitete.)
Folgerungen:
- Es gibt keine absolute Geschwindigkeit, sondern nur Geschwindigkeiten relativ zueinander.
Als Betrachter des Bildes mit den drei Raumschiffen und dem Laser wird man automatisch den Bildrahmen als Bezugssystem wählen. Es gibt aber kein absolutes Bezugssystem und keinen absoluten Raum. Die Aussagen, die man oft in Science-Fiction Filmen hört, das die Geschwindigkeit des Raumschiffes nun Null sei, ist deshalb falsch. Ein Raumschiff kann sich nur relativ zu einem anderen Körper z.B. einem Raumschiff oder Planeten nicht bewegen.
Lorentztranzformation und Äquivalenz von Masse und Energie
Aus den Axiomen der Speziellen Relativitätstheorie ergibt sich dann, daß die Ergebnisse vieler Experimente und Beobachtungen von der Relativgeschwindigkeit des Beobachters abhängig sind.
Insbesondere ergeben sich aus der Gleichheit der Lichtgeschwindigkeit in verschiedenen Inertialsystemen, dann die folgenden Eigenschaften von Zeit t, Länge L und Masse m in einem bewegten Bezugssystem, relative zur Zeit t0, Länge L0 und Masse m0 in einem ruhenden Bezugssystem.
Zeitdilatation - Relativität der Zeit
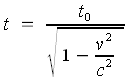
- t0 ist die Zeit, die ein Beobachter von einer Uhr abliest, der sich relativ zur Uhr in Ruhe befindet.
- t ist die Zeit die ein Beobachter von der gleichen Uhr abliest, der sich mit der Geschwindigkeit V, relativ zur Uhr bewegt.
- c ist die Lichtgeschwindigkeit.
Längen-Kontraktion oder Lorenz-Kontraktion
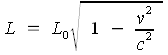
- L0 ist die Länge, die ein Beobachter für eine Strecke mißt, der relativ zu dieser Strecke ruht.
- L ist die Länge die ein Beobachter mißt, der sich mit der Geschwindigkeit V, relativ zu dieser Strecke bewegt.
- c ist die Lichtgeschwindigkeit.
Relativität der Masse
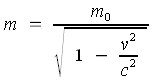
- m0 ist die Masse, die ein Beobachter mißt, der relativ zu dieser Masse ruht.
- m ist die Masse die ein Beobachter mißt, der sich mit der Geschwindigkeit V, relativ zu dieser Masse bewegt.
- c ist die Lichtgeschwindigkeit.
Äquivalenz von Masse und Energie
Man kann, mit Hilfe der Axiome der Speziellen Relativitätstheorie zeigen, das Masse eine Form von Energie ist. Die mit einer Masse verbundene Energie läßt sich über die folgende, wohl berühmteste Formel der Relativitätstheorie ausrechnen:
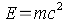
Da die Lichtgeschwindigkeit (c = 299 792,458 km/sec) einen sehr großen Wert hat, ergibt das Quadrat der Lichtgeschwindigkeit einen noch viel größeren Wert. Wenn man Masse in anderen Energieformen umwandeln kann, ergeben sich deshalb schon bei sehr kleinen Massen sehr große Energiewerte. Dies ist zB. der Grund dafür, das bei der Fusion von Wasserstoff zu Helium, in der Sonne, bei der ein kleiner Massendefekt auftritt, gewaltige Mengen von Strahlung in Form von Licht und Wärme erzeugt werden.
Der Minkowskiraum
s2 = c2t2 - (x2 + y2 + z2)
s ist der Abstand zwischen zwei Ereignissen.
| Albert Einstein: "Allgemeine Relativitätstheorie" |

|

|
Einleitung:
Die allgemeine Relativitätstheorie bezeichnet man auch als Einsteins Theorie der Gravitation, da sie den aus der Newtonschen Theorie folgenden Begriff des Gravitationsfeldes durch die Krümmung der Raumzeit ersetzt. Nach der Newtonschen Theorie üben zwei Massen aufeinander eine Kraft aus welche dazu führt, daß die Massen sich mit zunehmender Geschwindigkeit aufeinander zu bewegen, wenn sie nicht durch andere Kräfte daran gehindert werden (Fernwirkung).
Desweiteren beschäftigt sich die spezielle Relativitätstheorie nur mit Bezugssystemen die sich relativ zueinander mit konstanter Geschwindigkeit bewegen. Die Verallgemeinerung auf relativ zueinander beschleunigte Systeme erfolgt in der allgemeinen Relativitätstheorie.
Äquivalenzprinzip:
Die fundamentale Idee die zur allgemeinen Relativitätstheorie führt, ist die äquivalente Betrachtungsweise von Beschleunigung und Gravitation. (Äquivalenzprinzip)
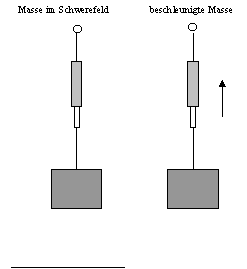
Konkret bedeutet dies, daß man in einem abgeschlossenen Raum nicht unterscheiden kann, ob man sich in einem "Gravitationsfeld" befindet, oder ob dieser Raum entsprechend beschleunigt wird.
Als Beispiel ist hier eine Federwaage dargestellt, die in einem Gravitationsfeld den gleichen Wert anzeigt, wie bei einer entsprechenden Beschleunigung.
Die Grundlegende Idee ist nun, Beschleunigung und Gravitation gleich zu behandeln, da diese sich in einem abgeschlossenen Raum, messtechnisch nicht unterscheiden lassen. Dies heißt zwei in der klassischen Physik unterschiedlich behandelte Phänomene werden zu einem einziges Prinzip zusammengeführt.
Der freie Fall und die Krümmung der Raumzeit
Wenn man sich anderseits, in einem geschlossenen Raum befindet, der sich im freien Fall auf einen Planeten ohne Atmosphäre zu bewegt, so gibt es innerhalb des Raumes keine Möglichkeit, die Beschleunigung relativ zur Position des Planeten zu messen.
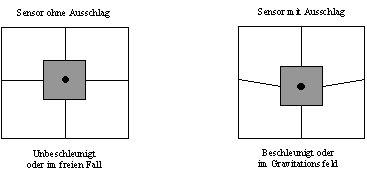
Sensor zum Messen von Beschleunigungen bzw. von Gravitaionsfeldern
In den beiden Zeichnungen des obrigen Bildes ist ein Sensor zum Messen von Beschleunigungen bzw. eines vorhandenen Gravitationsfeldes dargestellt. Der Sensor besteht aus einer Masse, die an vier Federwagen aufgehängt ist. (bzw. sechs wenn man Beschleunigungen in alle drei Dimensionen des Raumes messen will.)
Im ersten Bild ist ein Sensor dargestellt, der nicht beschleunigt wird oder sich im freien Fall in einem Gravitationsfeld bewegt. Die vier Federwaagen zeigen in diesem Fall keinen Ausschlag an.
Im zweiten Bild ist der gleiche Sensor dargestellt, wenn dieser beschleunigt wird oder der Sensor sich in einem Gravitationsfeld nicht bewegt. Zum Beispiel könnte der Sensor auf einem Labortisch auf der Erde stehen.
Nach der klassischen Physik befindet sich der Sensor relativ zum Tisch nicht in Bewegung. Nach der allgemeinen Relativitätstheorie misst der Sensor auf dem Tisch aber eine Beschleunigung.
In dem nachfolgenden Bild ist ein sehr spezieller Planet dargestellt, mit dessen Hilfe ich zeigen möchte, wie sich die Bewegung zweier Körper relativ zueinander, innerhalb eines Gravitationsfeldes, nach der allgemeinen Relativitätstheorie neu interpretieren läßt.
Der Planet soll keine Atmosphäre haben, da der Reibungswiederstand der Atmosphäre die Bewegung eines Körpers abbremst und dadurch eine Beschleunigung darstellt. Desweiteren soll der Planet nicht rotieren. Durch den Planeten sei ein Loch gebohrt, das so groß ist, daß zwei Probekörper, die beide mit einem Sensor zur Messung der Beschleunigung ausgestattet sind, ohne Probleme durch diesen Planeten hindurch fallen können.
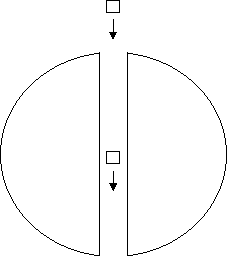
Zwei Inertialsysteme im "Gravitationsfeld"
Die beiden Probekörper kommen von einem Bereich im Weltraum, der sehr weit von unserem Planten entfernt ist. Die Schwerkraft unseres Planeten ist in dieser Entfernung vernachlässigbar klein. Die beiden Probekörber bewegen sich nun am Anfang mit gleichen Abstand in die Richtung unseres Planeten.
Der erste Probekörper wird aber stärker beschleunigt als der zweite Probekörper, wenn diese sich in die Richtung des Planeten bewegen. Der Abstand zwischen den beiden Probekörpern vergrößert sich deshalb. Wenn der erste Probekörper sich im Zentrum unseres Planeten befindet, hat er die maximale Geschwindigkeit und den maximalen Abstand. Danach wird der erste Probekörper wieder langsammer. Wenn die beiden Probekörper, wieder einen großen Abstand von dem Planeten erreicht haben, fliegen sie wieder mit der gleichen Geschwindigkeit und dem gleichen Abstand relativ zueinander, wie am Beginn des Experimentes.
Während der gesamten Durchquerung des Planeten haben die beiden Probekörpern mit ihren eingebauten Sensoren keine Beschleunigung gemessen. Ein Beobachter innerhalb dieser Probekörper würde schweben. Die beiden Probekörper haben aber die Möglichkeit die Entfernung relativ zueinander durch den Austausch von Lichtimpulsen zu messen. Nehmen wir weiter an, daß das Loch im Planeten sehr groß ist, und der Planet von den Probekörpern aus nicht gesehen werden konnte. Von den Probekörpern aus, konnte deshalb nicht festgestellt werden, das sie sich in einem Schwerefeld befanden. Eine Beschleunigung wurde in keinem der beiden Probekörper gemessen. Der Abstand zwischen den beiden Körpern hatte sich für die Zeit der Durchquerung des Planeten geändert, also ist der Raum in diesem Bereich des Universums gekrümmt.
Wir wollen nun einen kleinen abgegrenzten Raumbereich betrachten z.B ein kleiner Würfel mit dem Namen dV, der die folgenden Eigenschaften hat:
- Der Würfel dV bewege sich ungehindert in einem Gravitationsfeld. Der Würfel befindet sich also im freien Fall. Wobei man einen Sateliten, der die Erde umkreist als eine spezielle Form des freien Falls auffassen kann.
- Der Würfel dV sei so klein gewählt, das sich die Inhomogenitäten des Gravitationsfeldes vernachlässigen lassen.
- Mit dem Würfel dV sei ein Koordinatensystem fest verbunden, welches sich deshalb mit dem Würfel bewegt.
Wenn diese Anforderungen erfüllt sind, so stellt der Würfel ein Inertialsystem dar. Innerhalb dieses Systems gelten die Gesetze der speziellen Relativitätstheorie.
ds2 = c2dt2 - (dx2 + dy2 + dz2)
ds ist der Abstand zwischen zwei Ereignissen innerhalb des Würfels dV. Die Abstände dt, dx, dy, dz liegen innerhalb des Würfels.
Innerhalb eines Gravitationsfeldes haben wir also kleine Raumelemente definiert, innerhalb derer sich die spezielle Relativitätstheorie anwenden läßt. Damit haben wir eine Verallgemeinerung der speziellen Relativitätstheorie auf einen Raumbereich mit einem Gravitationsfeld. Innerhalb einer solchen verallgemeinerten Relativitätstheorie, gilt die spezielle Relativitätstheorie nur noch lokal. Die Transformation zwischen verschiedenen lokalen Inertialsystemen liefert Informationen über die Struktur der Raumzeit.
Einsteins Feldgleichung
Die Einsteinsche Feldgleichung ist die fundamentale Gleichung der allgemeinen Relativitätstheorie.
Man kann diese Gleichung wie folgt beschreiben:
Die Masse definiert die Krümmung der Raumzeit und die gekrümmte Raumzeit bestimmt die Bewegung der Masse.
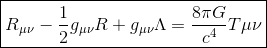
Die Einsteinsche Feldgleichung besteht aus den folgenden Elementen:
- Rμν ist der Ricci-Krümmungstensor
- R ist der Krümmungsscalar
- Λ ist die kosmologische Konstante
- G ist die Gravitations Konstante
- gμν ist der metrische Tensor
- c ist die Lichtgeschwindigkeit
- Tμν ist der Energie-Impuls Tensor
Die Einsteinsche Feldgleichung ist eine Tensorgleichung und besteht deshalb aus mehreren Einzelgleichungen. Jedem Element des Tensors entspricht eine Gleichung. Die einzelnen Elemente des Tensors und damit die einzelnen Gleichungen werden über die Indizies μ und ν definiert. Beide Indizes können jeweils die Werte von 0 bis 3 annehmen. Diese vier Werte repräsentieren die vier Dimensionen der Raumzeit. Dabei entspricht der Wert 0 der Zeit und 1, 2, 3 den x, y, z Achsen des Raumes. Von den 16 möglichen Varianten sind aber 6 Gleichungen Dublikate. Insgesamt hat man deshalb 10 Gleichungen für Berechnungen zur Verfügung.
Die linke Seite der Gleichung beschreibt die Krümmung der Raumzeit. Die rechte Seite der Gleichung hat mit der Verteilung von Masse und Energie zu tun.

|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|

|

|
| Physik | Mechanik | Elektrodynamik | Quantenmechanik | Konstanten | Physiker | Physik-Links | Farbenlehre | Abkürzungen | Mathematik |




