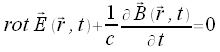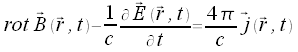|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|

|

|
| Physik | Mechanik | Raumzeit | Quantenmechanik | Statistische Physik | Konstanten | Physiker | Physik-Links | Farbenlehre |
| Prolog |

|

|
Van der Graaf Generator: "The least we can do is wave to each other."
| Elektrodynamik und Lorenzkraft |

|

|
Elektrodynamik
In der Elektrodynamik sind das elektrische- und das magnetische Feld die grundlegenden Größen. Das elektrische- und das magnetische Feld werden durch die Kraft definiert, welche diese auf eine punktförmige Ladung ausüben. Diese beiden Kräfte sind die komponenten der Lorenzkraft. Im Gegensatz zur Elektrostatik können sich die Felder in der Elektrodynamik auch zeitlich verändern.
Die nachfolgenden Gleichungen sind im Gaußschen CGS-System angegeben. Diese Gleichungen bekommen eine andere Form, wenn man ein anderes Einheitensystem, z.B. das SI-Einheitensystem verwendet.
Lorenzkraft
Die Lorenzkraft setzt sich aus zwei Komponenten zusammen. Die erste Komponente der Lorenzkraft ist die Kraft, welche von einem elektrischen Feld auf eine Ladung ausgeübt wird. Die zweite Komponente ergibt sich, wenn sich eine Ladung in einem magnetischen Feld bewegt.
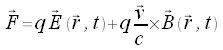
| Maxwellgleichungen |

|

|
Maxwellgleichungen
Die Maxwellgleichungen, sind zusammen mit der Gleichung für die Lorenzkraft, die Grundgleichungen der Elektrodynamik.
Dabei sind die Maxwellgleichungen die Feldgleichungen des elektromagnetischen Feldes. Diese sind partielle Differentialgleichungen. Die Ladungsdichte ρ (r,t) und die Stromdichte j(r,t) sind die Quellen des elektromagnetischen Feldes. Des Weiteren erzeugt ein sich änderndes elektrisches Feld ein sich änderndes magnetisches Feld und ein sich änderndes magnetisches Feld eins sich änderndes elektrisches Feld. Daraus ergibt sich die Existens der elektromagnetischen Welle.
Die Maxwell Gleichungen wurden von James Clark Maxwell im Jahre 1864 aufgestellt.
|
Coulombsches Gesetz |
|
Faradaysches Induktionsgesetz |
|
Nichtvorhandensein freier magnetischer Ladungen |
|
Ampersches Durchflutungsgesetz |
Da es keine magnetischen Monopole gibt, bzw. man noch keine gefunden gilt für das magnetische Feld:
![]()
Sollte man eines Tage magnetische Monopole finden, so bekommt diese Gleichung eine der Gleichung:
![]()
mit dem Quellterm für das elektische Feld entsprechende Struktur.
Kontinuitätsgleichung
Aus den Maxwellgleichungen lässt sich Kontinuitätsgleichung ableiten. => Ladungserhaltung.
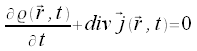
| Maxwellgleichungen in Potentialform |

|

|
Lorenz-Eichung
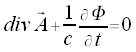
Maxwellgleichungen in Potentialform
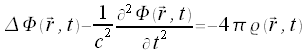
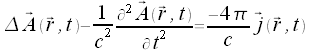
Mit der Hilfe der Viererpotentiale, der Viererstromdichte:
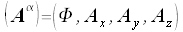
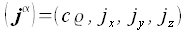
und des d'Alambert-Operators
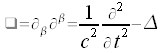
lassen sich die Maxwellgleichungen für die Potentiale in der folgenden Form darstellen:
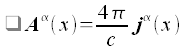
Vierervektoren
Die Orts- und Zeitkoordinaten lassen sich zu Lorenz- oder Vierervektoren zusammen fassen. Die indizes mit griechischen Buchstaben laufen von 0 bis 3.
Kontravarianter Vierervektor
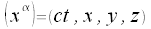
Der Operator der Differentiaton nach einer kontravarianten Komponente des Koordinatenvektors transformiert sich wie die Komponenten eines kovarianten Vektors.
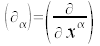
Kovarianter Vierervektor
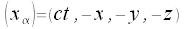
Der Operator der Differentiaton nach einer kovarianten Komponente des Koordinatenvektors transformiert sich wie die Komponenten eines kontravarianten Vektors.
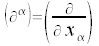
| Kovariante Darstellung der Maxwellgleichungen |

|

|
Aus den Maxwellgleichungen ergibt sich die Kontinuitätsgleichung:
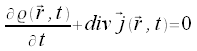
Mit Hilfe der 4-Stromdichte läßt sich die Kontinuitätsgleichung wie folgt umschreiben:
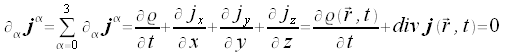
Dabei findet die Einsteinsche Summenkonvention Anwendung.
Feldstärke Tensor
Über die Viererpotentiale kann der Feldstärketensor wie folgt definiert werden:
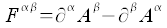
Daraus ergibt sich dann die folgenden Komponentendarstellungen des Feldstärke Tensors:
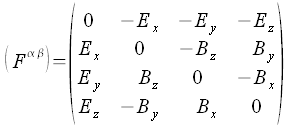
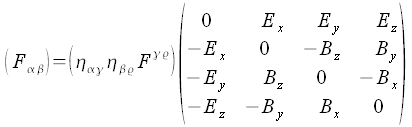
Dualer Feldstärketensor
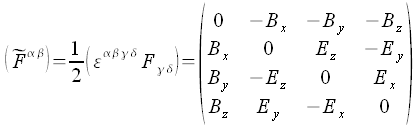
Kovariante Maxwellgleichungen
Über die obrige Definition der Feldstärke Tensoren lassen sich die homogenen und inhomogenen Maxwellgleichungen auf die folgende, elegante und kompakte Form bringen:
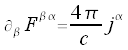
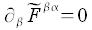

|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|

|

|
| Physik | Mechanik | Raumzeit | Quantenmechanik | Statistische Physik | Konstanten | Physiker | Physik-Links | Farbenlehre |