
|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|

|

|
| Physik | Elektrodynamik | Raumzeit | Quantenmechanik | Konstanten | Physiker | Physik-Links | Farbenlehre | Mathematik |
| Prolog |

|

|
| Newtons Axiome |

|

|
Lex prima
1.) Trägheitsgesetz:
Jeder kräftefreier Körper verharrt infolge seiner Trägheit (träge Masse) im Zustand der Ruhe oder geradlinig-gleichförmigen Bewegung (geradlinige Bewegung mit konstanter Geschwindigkeit).
Lex secunda
2.) Bewegungsgesetz:
Die zeitliche Änderung des Impulses eines Körpers ist gleich der auf den Körper einwirkenden Kraft.
Lex tertia
3.) Actio-Reactio-Gesetz:
Jede Wirkung ruft eine gleich große Gegenwirkung hervor.
Lex auarta
4.) Superpositionsgesetz der Kräfte:
Die Kräfte überlagern sich ungestört, d.h., die Addition der Kräfte erfolgt im Sinne des Kräfte-Parallelograms.
| Lagrangegleichungen der 1. Art |

|

|
Lagrangegleichungen der ersten Art
Sind die Bewegugen durch Zwangsbedinungen eingeschränkt, z.B die Bewegung findet nur auf der Oberfläche eines Tisches statt, so läßt sich der Lagrangeformalismus anwenden.
Es entstehen dabei Zwangskräfte, die sich mit dem Lagrangeformalismus berechnen lassen. Dafür müssen die entsprechenden Zwangsbedingungen gegeben sein.
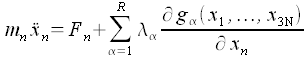 (n = 1, 2, ... , 3N)
(n = 1, 2, ... , 3N)
Zwangsbedingungen
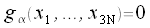 (α = 1, 2, ... , R)
(α = 1, 2, ... , R)
| Lagrangegleichungen der 2. Art |

|

|
Definition der Lagrangefunktion
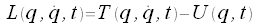
Die Lagrangefunktion wird als Differenz der kinetischen- (T) und der potentiellen Energie (U) definiert.
Lagrangegleichungen der zweiten Art
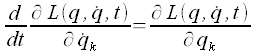 (k = 1, ... , f)
(k = 1, ... , f)
| Hamiltonformalismus |

|

|
Hamiltonfunktion
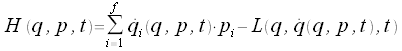
Hamiltonsche Gleichungen oder auch kanonische Gleichungen
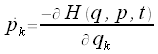 ,
,
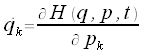

|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|

|

|
| Physik | Elektrodynamik | Raumzeit | Quantenmechanik | Konstanten | Physiker | Physik-Links | Farbenlehre | Mathematik |




