|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|

|

|
| Physik | Elektrodynamik | Mechanik | Raumzeit | Quantenmechanik | Konstanten | Physiker | Physik-Links | Farbenlehre |
| Prolog |

|

|
Asterix: "Alea iacta esto" (= Der Würfel soll gefallen sein!)
Arno Best: "Entropie braucht keine Wartung!"
| Einleitung |

|

|
Häufig ist es bei der großen Zahl von Teilchen, mit denen man es in der Physik zu tun hat gar nicht möglich, Aussagen über das Verhalten eines einzelnes Teilchen zu machen. Man denke nur an Materie im Gasförmigen Zustand. Für ein ideales Gas gilt, dass ein Mol bei Normalbedingungen (273,15 K, 101325 Pa) ein Volumen von 22,414 Litern hat. Durch die Avogadro-Konstante (6,022 136 7(36) * 1023 Teilchen pro Mol ) ist schon in einer kleinen Menge Gas eine gewaltige Anzahl von Teilchen festgelegt.
Es gibt aber auch grundsätzliche Grenzen. Bereits in der klassischen Mechanik ist das Resultate der Wechselwirkung durch die Gravitationskräfte, wenn mehr als zwei frei bewegliche Massenpunkte in diesem System vorhanden sind nicht in geschlossener Form lösbar. Versucht man die Flugbahnen von mehr als drei Massenpunkten durch eine Computersimulation zu berechnen, so ist die berechnete Flugbahn sehr empfindlich abhängig von der Bestimmung der Ausgangsgrößen wie Position oder Impuls des Teilchens, sowie der Genauigkeit des verwendeten Computerprogramms.
Dieses Problem ist von grundsätzlicher Natur. Es nutzt nichts die Ausgangsparameter immer genauer zu bestimmen und die Genauigkeit des Computersystems immer mehr in die Höhe zu treiben. Schon nach wenigen Iterationen summieren sich die kleinsten Abweichungen zu deutlich sichtbaren Werten.
Die Quantenmechanik ist eine statische Theorie. Die Lösungen der Schrödinger-Gleichung sind Wellenfunktionen, die man als Wahrscheinlichkeitsdichtefunktion interpretiert. Von daher besteht auch ein enger Zusammenhang zwischen Quantenmechanik und statistischer Physik. Im Grunde macht die Quantenmechanik nur statistische Aussagen darüber mit welcher Wahrscheinlichkeit ein Ereigniss eintritt.
| Wahrscheinlichkeit und Zufallsexperiment |

|

|
Beispiel: Als einfaches Beispiel eines Zufallsexperiments möchte ich hier das werfen einer Münze vorstellen. Die Münze habe auf der einen Seite einen Kopf und auf der anderen Seite eine Zahl. Beim werfen einer Münze habe ich als Ergebnis Kopf oder Zahl.
Den Fall, das die Münze auf dem Rand liegen bleibt, möchte ich hier ausschließen. Der Rand unserer Münze ist so rund, das diese auf dem Rand nicht liegen bleiben kann. Sie wir immer auf einer der beiden Seiten zum liegen kommen.
Für die abstrakte Darstellung einer Wahrscheinlichkeit wähle ich den Buchstaben P (im englischen heißt Wahrscheinlichkeit „Propability“). Für Wahrscheinlichkeiten wählt man üblicher Weise einen Zahlenwert zwischen 0.0 und 1.0. Wobei der Wert 1.0 bedeutet, das dies Ereignis bei jedem Experiment eintritt. Der Wert 0.0 bedeutet, das dieses Ereignis nie eintritt.
Für unser Münzen Beispiel nehmen wir an, das die beiden möglichen Ereignisse, Kopf K oder Zahl Z mit der gleichen Wahrscheinlichkeit auftreten. Wir setzen deshalb die folgenden Werte:
Wahrscheinlichkeit Kopf zu werfen: P(K) = 0.5
Wahrscheinlichkeit Zahl zu werfen: P(Z) = 0.5
Die Möglichen Ergebnisse eine Experiments fasst man als Ergebnismenge zusammen.
E = {K, Z}
| Grundlegende mathematische Konzepte der Statistik |

|

|
Definition der Wahrscheinlichkeit
In der Mathematik wird die Wahrscheinlichkeit eines Ereignisses A durch eine reelle Zahl im Bereich von 0.0 bis 1.0 definiert. Ein unmögliches Ereignis hat die Wahrscheinlichkeit 0 und ein sicheres Ereignis die Wahrscheinlichkeit 1.
Nimmt man an, dass alle Ergebnisse eines Zufallsexperimentes mit der gleichen Wahrscheinlichkeit auftreten, so kann man die Wahrscheinlichkeit für das Auftreten eines bestimmten Ereignisses A wie folgt definieren:
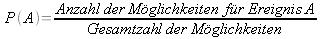
Kombination von Wahrscheinlichkeiten
Wenn man die Wahrscheinlichkeit P(A) für das Auftreten eines Ereignisses kennt so ergibt sich die Wahrscheinlichkeit dafür, das dies Ereignis nicht auftritt über die folgende Formel:
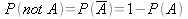
Wenn zwei Ereignisse A und B von einander unabhängig sind so gelten die folgenden Säte:
Die Wahrscheinlichkeit für das gleichzeitige auftreten von zwei Ereignisse A und B ergibt:
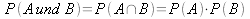
Oder allgemein:
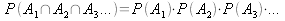
Die Wahrscheinlichkeit dafür, das sowohl A oder B auftreten können gilt:
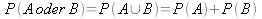
Oder in allgemeiner Schreibweise:
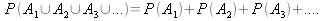
| Grundlegende mathematische Konzepte der Statistik |

|

|
In Bearbeitung

|
Home | Gallery | Philosophie | Software | Musik | Kunst | H.Wacker | Links | Inhalt |
 English
English

|

|

|
| Physik | Mechanik | Elektrodynamik | Raumzeit | Quantenmechanik | Konstanten | Physiker | Physik-Links | Farbenlehre |