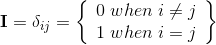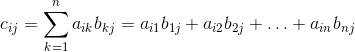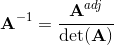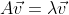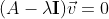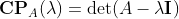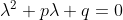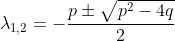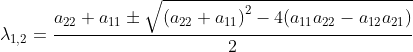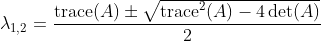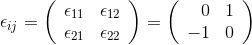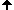Prolog

This page has been developed to support my Geometric Algebra page and on my Clifford Algebra page. The relations between Geometric Algebra and Matrices are explored on my Geometric Algebra and Matrices page.

Geometric Algebra

Clifford Algebra

Geometric Algebra and Matrices

Attention

This page has been tested and developed with the Mozilla browser. This page requires JavaScript in your browser. Without JavaScript or JavaScript beeing disabled, the display of this side is incomplete.

Matrices

A matrix A is a rectangular array of a_ij elements. The index values i and j define the position of the element in the matrix. The i value defines the row value and the j value defines the coulumn value. A matrix can have m rows and n columns:

By default the elements a_ij of a matrix are real numbers. If the elements are from a different kind, this will be stated, or it becomes clear from the context in which the matrix is used. Sometimes the following shortform for a matrix is used:

A = a_ij

The element a_ij with variable indices ij is used as Symbol for all elements of a matrix.

Matrix Examples:

Special Matrices

Column Vector

Matrices with only one column are called column vectors.

Row Vector

Matrices with only one row are called row vectors.

Vectors and Matrices

A general vector can be written in the form a = a_i. The information if it is a column vector or a row vector is only neccessary if the vector elements are interpreted as a matrix.

Quadratic Matrices

If the number of rows and the number of columns of a matirix are the same, the matrix is called a quadratic matrix:

Unit Matrix

A unit matrix I_n is a quadratic matrix where all the diagonal elements are one and all the other elements are zero.

Kronecker Delta

The Kronecker Delta is a function that depends on its two indices as variables.

The elements of a Unit Matrix can be defined with the Kronecker Delta. The Kronecker Delta defines an matrix element value depending on the element position by the following rules:

Where i and j define the position of the matrix element.

In the case of a quadratic matrix the result of the Kronecker Delta function will be the unit matrix.

Single Entry Matrix

A single entry matrix e_ij is a matrix where a single element e_ij is one and all the other matrix elements are zero.

Example Base Vectors and Unit Matrix

The Base vectors e₁, e₂, e₃ can be interpretated as column vector with a single entry:

Basic Matrix Operations

Matrix Additon and Subtraction

When two matrices have the same number of lines and columns it is possible to perform the additon and the subtraction of two matrices. In this case the sum of two matrices is build by adding the matrix elements and the difference is build by subtracting the matrix elements.

A+B = a_ij + b_ij;    A-B = a_ij - b_ij;

Example:

Multiplication with a Scalar

The multiplication of a Matrix A with a scalar λ is the same as multipling each element a_ij of the matrix with a scalar λ.

λA = λa_ij

Example:

The Transposed of a Matrix

The transposed of a matrix is defined by echanging the columns and the rows of a given matrix.

A^T = (a_ij)^T = a_ji

Examples:

The transposed of a matrix is a matrix where the elements of the original matrix are mirrored at the diagonal:

Applying the operation of a transposition twice on a matrix, will result in the original matrix.

A^TT = (a_ij)^TT = (a_ji)^T = a_ij = A

Symmetric Matrices

A matrix is symmetric if A = a_ij = a_ji = A^T. that means a matrix A is equal to its transposed.

Example:

Matrix Product

The matrix product is not commutative. If A and B are matrices, then the product AB≠BA. The matrix product is only defined if the number of columns of the first matrix A is the same as the number of rows of the second matrix B. The product of the matrixes A and B defines a new matrix AB=C. The elements c_ij of the matrix C are defined by the following formular:

Special Matrix Products:

Matrix product of the the row vector A with the column vector B where both vectors A and B have two elements.

The Product of a row vector A with a column vector B will be the Matrix C which has only one element called c₁₁.

AB=C=(c₁₁)=(a₁b₁+a₂b₂);    c₁₁=a₁b₁+a₂b₂;

The result is the scalar product of the two vectors.

The product of a column vector with a row vector BA=D.

The result of the matrix product BA is a 2×2 matrix.

Redefining A and B to row and column vectors with 3 elements:

AB=C=(c₁₁)=(a₁b₁+a₂b₂ + a₃b₃);    c₁₁=a₁b₁+a₂b₂+ a₃b₃;

The result of the matrix product BA is a 3×3 matrix.

Examples - Matrix Products:

Product of the matrices A and B.

Other Matrix Operations

Single Entry Matrix

A single entry matrix e_ij is a matrix where a single element e_ij is one and all the other matrix elements are zero.

The Base vectors e₁, e₂, e₃ can be interpretated as column vector with a single entry:

Example:

Extracting columns out of a matrix.

Applying unit vectors e₁, e₂, e₃ to a matrix for column extraction.

Row Addition Transformation

L_ij(a) = I + ae_ij (i≠j)

Row Switching Transformation

T_ij = I + e_ij + e_ji - e_ii - e_jj

Row Multiplying Transformation

D_i(a) = I + (a-1)e_ii (a≠0)

Generalising Vectors and Matrices to Tensors

The rank value defines the number of indices an element a can have. An element without index is a scalar. The general name for an element with multiple indices is tensor.

Rank	Element	Name	Tensor
0	a	scalar	tensor rank 0
1	ai	vector	tensor rank 1
2	aij	matrix	tensor rank 2
3	aijk		tensor rank 3
...	aijk...		tensor rank ...

Permutation

In general a permutation is a rearrangement of elements of an ordered list like the elements of a vector. Permutations can be expressed as matrix operations on a vector. If an arrangement contains n elements n! different permutations are possible.

Permutaions as Matrix Operations

A permutation is a matrix operation that leads two the exchange of the elements of a vector, when the matrix is multiplied with the vector.

The unit matrix is a permutation matrix, that leaves the order of the vector elements unchanged when applied to the vector.

Exchange Matrix

The exchange Matrix is the next example of a permutation matrix.

The exchange matrix or counterbrace matrix J_n, is a matrix where the counterdiagonal elements are all one. All other elements are zero.

The product of the exchage matrix with a column vector will result in a reordering of the column elements. The product of a row vector with a exchange matrix will result in a reordering of the row elements.

Square of the Exchange Matrix

J² = I

The square of the exchange matrix is the unit matrix. Applying the exchange matrix twice will result in the original matrix.

Transpositions

Transpositions are permutations where only two rows of a matrix are exchanged. Every permutation can be expressed as a product of transposions.

Transpositions with a 2*2 matrix:

With two elements 2! = 2 permutations are possible.

Transpositions with a 3*3 matrix

With three elements 3! = 6 permutations are possible.

Determinant

A determinant is a linear function that calculates a scalar value from the elements of a quadratic matrix.

Algorithems for calculating the value of a Determinant

The determinant of a one dimensional matrix contains only one element. The result of the determinant operation is the value of this element:

The determinant of a two dimensional matrix is calculated as follows:

The determinant of a three dimensional matrix can be developed after the first Line:

Also the determinant of a four dimensional matrix can be developed after the first Line:

In this manner a determinant of any dimension can be developed after the first line by building the determinants of the minor matrices. For detail look for the description in the minor section.

Determinant Examples:

Properties of a determinant

A determinant det(A) of an n×n matrix A captures the signed volume of an n-dimensional parallelepiped whose sides are the columns of A.

Determinants and the Outer Product

Minors

A submatrix A_ij of a matrix A is the matrix that is received by deleting the i^th row and the j^th column of the matrix A.

Example:

The minor M_ij = |A_ij| is the determinant of the submatrix A_ij.

Example:

Calculation of a Determinant with Minors

With the help of the minors it is possible to calculate the determinant of a matrix A.

Example: Development after the first row of A:

Relations of a Determinant to it's Minors

With the help of the following formulars it is possible to define the following relations between a determinant and its minors:

Delevopment when a constant row i is selected.

Delevopment when a constant column j is selected.

Cofactors

The cofactor C_ij is obtained by multiplying the minor M_ij by (-1)^i+j.

Examples:

The signum of a 4 x 4 matrix:

The Cofactor matrix of a 3 x 3 matrix:

Relations to the Determinant to its Cofactors

Delevopment of a determinant when a constant row i is selected.

Delevopment of a determinant when a constant column j is selected.

The Adjugate Matrix or Classical Adjoint Matrix

The adjugate matrix adj(A) of a quadratic matrix A is the transposed of the cofactor matrix: adj(A) = C^T = (-1)^j+iM_ji

The Invers of a Matrix

The inverse of a quadratic matrix A is denoted as A^-1. The product of a matrix A with its inverse matrix A^-1 shall be the unit matrix 1.

AA^-1 = 1

Not every matrix is inveritable. It is required that the determinant of a matrix A is not equal zero, det(A) ≠ 0 for the existens of an invers matrix.

A matrix that has no inverse, is called singular or non regular.

If a inverse matrix can be defined, it will have the following properties:

AA^-1 = A^-1A = 1

That means that the product of the matrix A with its invers A^-1 is commutative.

Calculating the Invers

When the adjungated matrix A^adj of a matrix A and the dererminant det(A) of a matrix A is given, the invers of a matrix A can be calculated by dividing each element of the adjungated matrix A^adj by the value of the determinant det(A):

The above formular requires that det(A) ≠ 0.

Example:

Example:

Product of two matrices

If A and B are n×n matrixes and both are invertialbe then (AB)^-1 = B^-1A^-1

Proof: Multiplying both sides with AB from the left gives:

AB(AB)^-1 = ABB^-1A^-1= A1A^-1 = AA^-1 = 1;

Product of three matrices

(ABC)^-1 = C^-1B^-1A^-1

Proof: Multiply both sides with ABC from the left.

Similar Matrices

Two n×n matrices A and B are called similar if an invertibal n×n matrix P exists so that:

B = P^-1AP

Example:

Linear Transformation

Example

The product of a matrix A with a vector v results in the vector w. This product is a linear transformation of the vector v into the vector w.

Av = w

Definition

A transformation T(v) is linear if the following two conditions hold:

(i)  λT(v) = T(λv).

(ii) T(u) + T(v) = T(u+v).

If the basic vectors of a vector space are known and the dimension of the vector space is finit a linear transformation can be expressed as a matrix:
T(v) = Av.

Example

Linear Equation Systems

Let A be a n×n matrix and x and b are column vector with n elements. Then a linear equation system can be written in the following form as matrix equation:

Ax = b

Example

A linear equation system:

Solutions of Linear Equation Systems

If A is an invertiable n×n matrix, then the equation Ax = b has a unique solution x∈𝕍ⁿ for any b∈𝕍ⁿ.

A matrix is invertiable if a inverse matrix A^-1 exist with AA^-1 = A^-1A = I.

A matrix A is invertibable. ⇔ det(A) ≠ 0;

Ax = b

Multiplying from the left with A^-1:

A^-1Ax = A^-1b;

Ix = A^-1b;

x = A^-1b;

Example

Cramer's Rule

We have a linear equation system with n equations written as matrix product. Where A is a n×n matrix and the column vectors x and b have n elements.

Ax = b

If the determinanat of A is det(A) ≠ 0 then Cramer's Rule can be applied. Cramer's rule states that the unknown elements x_i of the vector x can be calculated by the following formular:

The matrix A_i is defined by replaceing column vector i of A by the column vector b.

Example:

We have the relation Ax = b. Using the following elements, x can be calculated if A and b are known:

Further Properties of the Determinant

Let A, B and P be n×n matrices.

Unit Matrix

det(I) = 1;

Product of Matrices

det(AB) = det(A)det(B);

Invertibal Matrices

If A is invertiable:

A^-1A = I;

det(A^-1)det(A) = det(I) = 1;

det(A^-1) = 1/det(A);

Diagonal Matrices

The determinant of a diagonal matrix is the product of the diagonal elements.

Example:

Similar Matrices

The determinant of a similar matrix is equal to the determinant of the original matrix. The similar transformation of a matrix A does not change the value of the determinant.

det(B) = det(P^-1AP) = det(P^-1)det(P)det(A) = det(A);

Scalar Multiplikation

Let λ be a scalar value and A be a n×n matrix and each element of A is multiplied with λ then the following relation for the determinant exists:

det(λA)= λⁿdet(A);

Transposed Matrices

The determinant of a transposed matrix is equal to the determinant of the original matrix.

det(A) = det(A^T);

The transposition of a matrix exchanges row and columns. For each row operation on determinants matrix an equivalent column operation can be found.

Exchangeing Rows or Columns of a Matrix

Exchanging two neighbor rows or neighbor columns of a matrix will change the sign of the matrix:

Multiplying with a Factor

If you multiply the matrix with the factor k will be the same as if you multiply a row or a column of the matrix with k

The Determinant is Zero

If the column(row) vectors are not linear independent, the determinant will be zero.

If all elements of a line or a column are zero the value of the determinant will be zero.

If a two columns or two rows of a determinant have the same values, then the determinant will be zero.

If a row (column) of determinant is the linear combination other rows (columns), the value of the determinant is zero.

Sum of Row or Column Vectors

If a column or row of a determinant is interpreted as the sum of two column or two row vectors then the matrix can be interpreted as the sum of two determinants where each determinant contains only one part of the sum.

Unchanging Transformations

Adding the multiple of a row(column) of a determinant to another row(column) does not change the value of the determinant:

Determinant of a Triangular Matrix

The value of the determinant of a triangular matrix is the product of the diagonal elements of the matrix.

Matrices with Complex Elements

Complex and Conjungated Complex Numbers

The complex conjugation changes the sign of the imaginary part of a complex number.
If z = a + ib is a complex number, then the conjugated complex number relative to z is written as z = a-ib.

Product of a Complex Number with it's Conjungated Value

The product of a complex number z with the conjugated value z gives a real number:

zz = zz = (a+ib)(a-ib) = (a-ib)(a+ib) = a² + b²;

Adjoint Matrix

The adjoint of a matrix is build by calculating the transposed of a matrix and conjugate its elements.

A adjoint matrix of a matrix A is denoted A^*.

Adjoint Example

Let z be a vector with complex elements. The adjoint of z is z^*

Hermitian Matrix

A Hermitian matrix (or self-adjoint matrix) is a quadratic matrix with complex elements that is equal to its adjoint matrix. A = A^*

The matrix A is hermitian, if a_ij = a_ji.

Example Hermitian Matrix

Rotation Matrices

If R is a n×n matrix and the value of the determinant of R; det(R) = 1; then R is a rotation matrix.

Multiplying the rotation matrix R with the vector v which has n elements will result in a vector v'.

v' = Rv

A rotation matrix R change only the direction of a vector v when this vector is multyied with the matrix R and leave the length of a the vector v unchanged:

|v'| = |Rv| = |v|

2×2 Rotation Matrices

Let the rotation matrix have the following form:

More Information about rotation matrices can be found on the rotation matrix side.

Rotation Matrices

Eigenvalues and Eigenvectors

Let A be the square matrix of a linear transformation. Wenn a vector v exists (v ≠ 0) that is unchanged or is only changed in length when v is multipied with the matrix, then this vector v is an eigenvektor of the matrix A. The scaling factor λ of the vector is called an eigenvalue of the matrix A.

Eigenvalue Equation:

With A being a square matrix and λ being eigenvalues (scalar values) and v being eigenvector.

Example:

Characteristic Polynomial

Rearanging the Eigenvalue Equation gives:

Example:

Building the determinate of the first term in this expression will give in the characteristic polynomial CP_A(λ)

With the help of the characteristic polynomial it is possible to compute the eigenvalues of a matrix.

Example:

Let A be a 2*2 matrix

In the case of a 2*2 matrix the charactaristical polynomial CP_A(λ) can be written in the following form:

CP_A(λ) = λ² - trace(A)λ +det(A);

A trace is the sum of the diagonal elements of a matrix. The solutions of this quadratic equation are the eigenvalues λ.

A general quadratic equation:

has two solutions:

for the characteristic polynomial CP_A(λ) of a 2*2 matrix we have:

p = -(a₂₂+a₁₁) = -trace(A)

q = a₁₁a₂₂ - a₁₂a₂₁ = det(A)

From this we get the following two eigenvalues λ_1,2

In the case of a 2*2 matrix A we have the following two eigenvalues expressed with the trace and the determinate of the matrix A:

Example:

trace(A) = -6+5 = -1

det(A) = -6*5 - 3*4 = -42

CP_A(λ) = λ² + λ - 42 = 0;

Calculating the eigenvalues λ_1,2

λ₁ = (-1 + sqrt(1 + 4*42))/2 = (-1 +13)/2 = 12/2 = 6

λ₂ = (-1 - sqrt(1 + 4*42))/2 = (-1 -13)/2 = -14/2 = -7

Calculating the Eigenvectors

Eigenvector for λ₁=6;

Linear independent Eigenvectors

Eigenvectors that belong to different eigenvalues are linear independent.

Eigenvalues and Eigenvectors in Similar Matrices

A matrix B is similar to a matrix A if an invertible matrix P exists that defines B with B = P^-1AP.

An n×n matrix A is similar to diagonal matrix L, if A has n linear independent eigenvectors. The diagonal elements of L are the eigenvalues. The eigenvectors are the column vectors of P.

Example:

Characteristic Polynomials of Similar Matrices

Similar matrices have the same characteristic polynomial. The converse however is not true in general. Two matrices with the same characteristic polynomial need not to be similar.

The matrix A and its transposed have the same characteristic polynomial.

Eigenvalues of a Triangular Matrix

If A is a triangular matrix, then the eigenvalues of A are the diagonal elements of A.

Cayley Hamilton Theorem

Every square matrix A fulfills its own characteristic polynomial, if the Matrix A is inserted in the charactaristic polynomial instead of λ.

CP_A(A) = 0

With 0 being a zero matrix.

Example

The matrix A has the following characteristic polynomial:

CP_A(λ) = λ² - 8λ +13 = 0

Inserting A instead of λ. The result is a zero matrix.

Eigenvectors of Symmetric Matrices

Eigenvectors x and y of symmetric matrix S are orthogonal.

S = S^T has orthogonal eigenvectors x^Ty = 0.

We have the following elements:

How to show orthogonality => x^Ty= 0 of the two eigenvectors x and y

If we transpose Sx = λx we get => x^TS^T = λx^T

If we use S^T = S we get => x^TS = λx^T

Multiplying from the right with y results x^TSy = λx^Ty

We can also multiply Sy = αy with x^T to get x^TSy = αx^Ty

Because λ≠α, x^Ty must be zero.

Decomposition of Symmetric Matrices

A symmetric matrix S can be writen in the following form:

S = QΛQ^T

With Q being the matrix of the eigenvectors of S and Λ is the matrix with the eigenvalues as diagonal elements.

For ortogonal eigenvectors the inverse of the Q matrix, is equal to the transposed of Q.

Q^-1 = Q^T.

Example

Definite Matrices

Definition

Let A be a symmetric n×n matrix with elements from ℝ.

Let x be a column vector with n elements from ℝ and x ≠ 0 ⇔ x ∈ ℝⁿ and x ≠ 0.

Then x^TAx will be a scalar value from ℝ.

Remark

Symmetric matrices have real eigenvalues.

The eigenvectors of a symmetric matrix are orthogonal.

Example

Definitions

If for all x ∈ ℝⁿ and x ≠ 0 and A being a symmetric n×n matrix:

x^TAx > 0 ⇒ matrix A is poitive definite.

x^TAx ≥ 0 ⇒ matrix A is poitive semi definite.

x^TAx < 0 ⇒ matrix A is negative definite.

x^TAx ≤ 0 ⇒ matrix A is negative semi definite.

If the result od x^TAx is neither poitive semi definite nor negative semi definite for all x the matrix is called indefinit.

Single Value Decomposition

Each m×n Matrix A can be transformed into the product of three matrices:

A = USV^T

U is a m×m matrix; S is m×n matrix and V is a n×n matrix.

From a m×n Matrix A the products A^TA and AA^T can be constructed. These two matrices have the following properties:

• The two matrices are symmetric.
• Both matrices are square matrices.
• They are positive semidefinit (eigenvalues are zero or positive).
• Both matrices have the same positive eigenvalues.
• Both matrices have the same rank as A.

Example:

The two matrices are symmetric hence the eigenvectors are orthogonal. So orthonormal eigevectors can be choosen.

The eigenvectors of AA^T are named u_i

The eigenvectors of A^TA are named v_i

These sets of eigenvectors are called u and v and are called the singular vectors of A.

Both matrices have the same positive eigenvalues.

The square roots of these eigenvalues are called singular values.

The matrix U is constructed by the u_i as column vectors. U = (u₁ ... u_m).

The matrix V is constructed by the v_i as column vectors. V = (v₁ ... v_n).

U^TU = I

V^TV = I

Singular Value Matrix S

A singular value matrix is a matrix, that contains the singular values σ_i on the diagonal.

The singular values are in the range of 1 to r, where r is the rank of A.

The singular values σ_i are the square root of the eigenvalues λ_i.

Example:

Example Singular Value Decomposition

The example matrix A can be decomposed in the product of three matrices.:

Levi-Civita-Symbol

The Levi-Civita-Symbol also known as the total antisymetric tensor or ε-tensor is a function of the values of its indices.

A specific Levi-Civita-Symbol for a specific permutation of its indices has to be defined for a specific value n. And has then n indices, where each index values can lay in a range between 1 and n.

The exchange of two index elements is called a transposition. The exchange of two index elements will result in a change of the sign of the epsilon tensor.

The general form of the ε_ij...k tensor is defined as follows, it also holds if two indices are the same (none distinctive elements).

A permutation is even if a even number of index transpositions has to be executed to get the permutation of 1,2...,n.

A permutation is odd   if a  odd number of index transpositions has to be executed to get the permutation of 1,2...,n.

If t is the number of transpositions to get a a specific permutation of distinctive index elements, then: ε_{ij...k =} (-1)^t

Example:

In 2-Dimensions the possible values can be presented in matrix form:

In 3-Dimensions the result can be thought of as staging of three matrices.

For relations between the Levi-Civita-Symbol and geometric algebra visit my geometric algebra page.

Levi-Civita-Symbol and Geometric Algebra

Kronecker Product

The Kronecker product is defined for two matrices and and will result in a third matrix. For the Kronecker product the symbol ⊗ is used:

A⊗B = C

The elements c_ij of the matrix C are again matrices and are calculated according to the following formular:

a_ijB = c_ij

Examples

The next page is about vectors.

Vectors