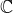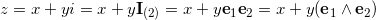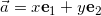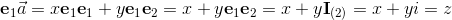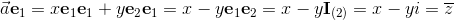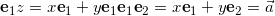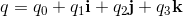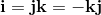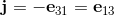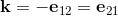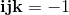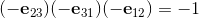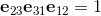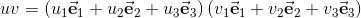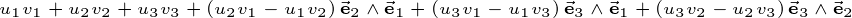Introduction
Geometric algebra introduces new geometric elements between which algebraic relations exists.
In addition to the well known scalar and vector elements these are bivectors, trivectors n-vectors and multivectors which
are generalisations of the well known vectors.
It also introduces new products like the outer product and the geometric product.
Geometric Algebra Basics
| Scalar |
Vector |
Bivector |
Trivector |
4-Vector |
... |
n-Vector |
| 1 |
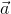 |
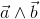 |
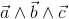 |
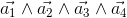 |
... |
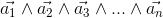 |
|
 |
 |
 |
|
|
|
The main elements of geometric algebra can be found in the above table.
Geometric algebra introduces in addition to the well known scalar values and vectors further elements.
The elements are called n-vectors or blades. For the first two n-vectors we have the name bivector and trivector.
This elements can be seen as a directed area in the case of a bivector and as a directed volume in the case of the trivector.
The scalar product is sometimes visualised as a dot at the origin.
Scalars
Scalars are the well known rational (real) numbers like 0, 1, 2.5, 3.1415... .
Vector

A vector is an oriented length.
More on vectors on the vector page:
Vectors
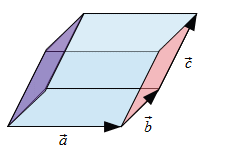
Bivector - The Outer Product of Two Vectors
A bivector or 2-vector is the first new fundamental buliding block of geometric algebra I like to present. A bivector can be generalised to
represent a plane in any dimension. No ortogonal vector is required. The plane is defined by the vectors that lay in the plane.
A Bivector: 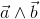 can be visualised by an oriented area that is spanned by two vectors:
can be visualised by an oriented area that is spanned by two vectors:
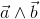 =
= 
A bivector is an oriented area element. It is descriped by the area and the orientation of the plane.
Many different vectors can be used to define the same oriented area in the same plane. So the form of a bivector must not be that of a trapezium that is spanned by
the two vectors. The same bivector can have many different forms, but must have the same area value and the same orientation.
The outer product is anticommutative.
When the order of the vectors a and b is exchanged the sign changes to the opposit value:
Also the orientation of the plane defined by the two vectors changes to the opposite direction,
if the two vectors building a bivector are exchanged:
If the two orthogonal unit vectors e1 and e2 lay in the same plane
as the vectors a = a1e1 + a2e2; and b = b1e1 + b2e2;
the outerproduct can be evaluated by the following equations:
The orthogonal unit vectors of the plane e1 and e2
define the unit bivector e1∧e2 of the plane.
The unit bivector e1∧e2 is a new base element of the plane.
The determinate defines the area of the bivector.
Through the evaluation of the determinante the area is defined. The same area value and the same orientation can be constructed in many different ways.
So the form of a bivector is not unique.
Trivector
A trivector 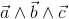 is an oriented volume.
is an oriented volume.
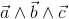 =
= 
n-vector
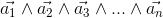
A n-Vector is an oriented n-dimensional volume.
Geometric Product
Geometric algebra introduces a new product called the geometric product. The geometric product of two vectors a and b is written ab.
The geometric product of two vectors is the sum of the scalar product and the outer product (bivector) of the vectors a and b.
The geometric product is invertiable. It is possible to divide by a vector.
With the geometric product, geometric algebra is a division algebra. The dimension of the vector is not limited.
Geometric algebra is a division algebra in arbitrary dimension.

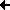
 English
English


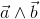 or a wedge b.
Graßmann published his book in the same year as Hamilton anounced the discovery of the quaternions. But did not receive
the same fame as Hamilton during his lifetime. Perhaps he was not taken seriously by his contempories because he was only a high school teacher.
or a wedge b.
Graßmann published his book in the same year as Hamilton anounced the discovery of the quaternions. But did not receive
the same fame as Hamilton during his lifetime. Perhaps he was not taken seriously by his contempories because he was only a high school teacher.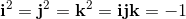

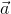
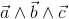
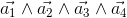
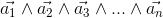



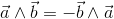
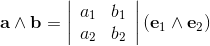
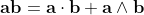
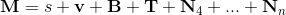
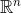 .
.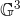
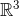
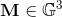 is build from a scalar, three vectors, three bivectors and one trivector.
is build from a scalar, three vectors, three bivectors and one trivector.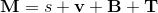
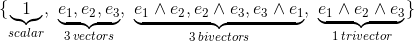
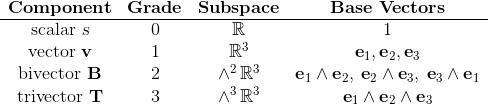
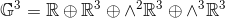
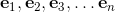 .
.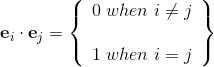
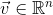 has the following decomposition in base vectors ei.
has the following decomposition in base vectors ei.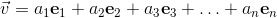
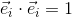
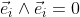
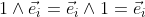
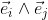
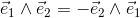
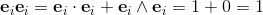
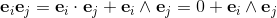
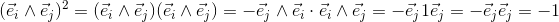
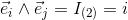
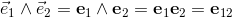
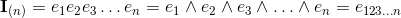
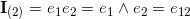
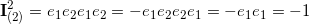
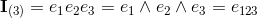
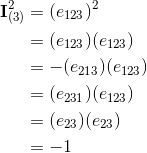
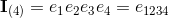
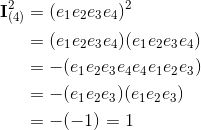
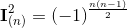
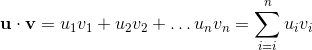
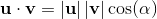
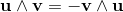
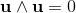
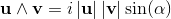
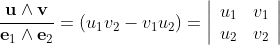
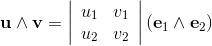
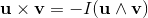
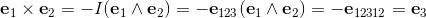
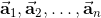
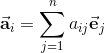
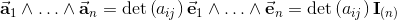
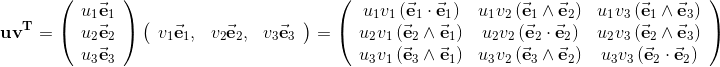
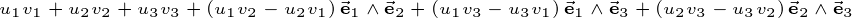
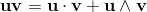
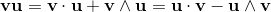
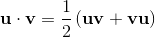
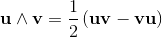
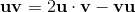
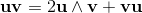
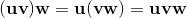
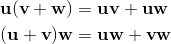
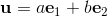
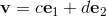
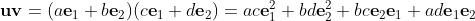
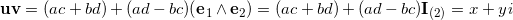
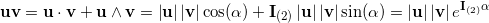
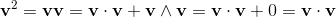
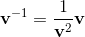
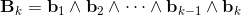
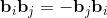
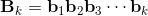
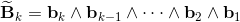
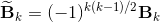
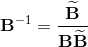
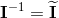
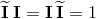
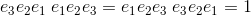
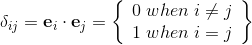

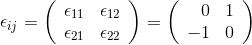

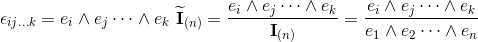
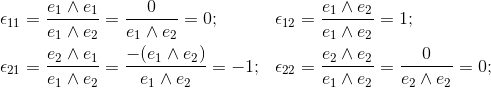
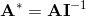
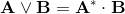
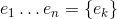
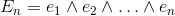
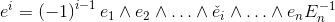
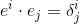

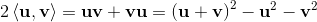
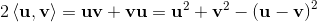
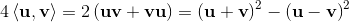
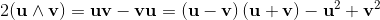
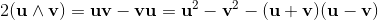
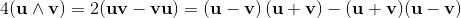
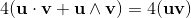
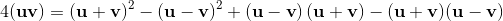
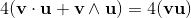
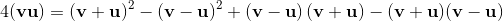

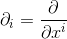
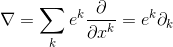
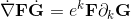
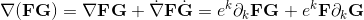
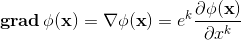
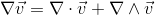
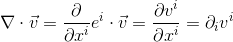
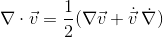
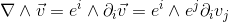
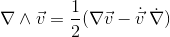
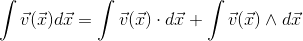
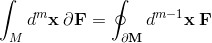

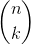 base elements (k-vectors) of grade k.
base elements (k-vectors) of grade k.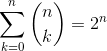



 and complex numbers
and complex numbers