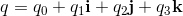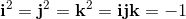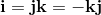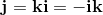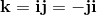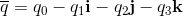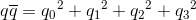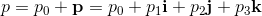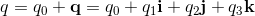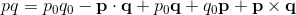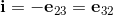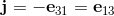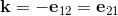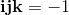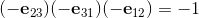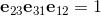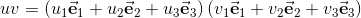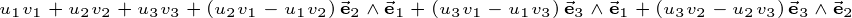Attention

This page has been tested and developed with the Mozilla browser. This page requires JavaScript in your browser. Without JavaScript or JavaScript beeing disabled, the display of this side is incomplete.

Prolog

What is the square root of -1?

Hypercomplex Numbers

a_k's are real numbers, i_k are different complex units with the property (i_k)² = -1 for all k.

Basic Matrices and Complex Numbers

The following 2x2 matrices can be used to construct a matrix representation of the complex numbers and a matrix representation of the quaternions.

With the basic properties: U² = I; H² = I; B² = -I

These are the same Matrices that where used for reflection and 90 degree rotation on the rotation matrix page.

Matrix Representation of Complex Numbers

The matrix equation z = xI + yB is isomorphic to the complex numbers. For more Information on these matrices see chromogeometry on my Geometric Algebra and Matrices page. For information of the realation between geometric algebra and complex numbers see my geometric algebra page.

With these matrices it is also possible to represent the geometric algebra 𝔾² in matrix form. With the base vectors as matrices: e₁ = U; e₂ = H; e₁₂ = B.

These Matrices are also used to perform basic reflections and 90° rotations in the plane.

Quaternions

Quaternions are elements of the Form:

q₀, q₁, q₂, q₃ are real numbers. i, j, k are three different square roots of -1 and are the new elements used for the construction of quaternions. They have the following algebraic properties:

Algebraic Properties

From this fundamental relations we get:

From this relations a multiplication table can be constructed.

Multiplication Table

Complex Conjugate of a Quaternion

Square of the Length

The Product of two Quaternions

The Relation between Quaternions and Geometic Algebra

The basic elements i, j, k of the quarterions can be indentified with the following bivectors in geometric algebra.

The elements i, j, k form a left handed System.

On the other hand if I build the product of bivectors for a right handed system I get:

If we build the geometric product of two vectors u and v from

Will result in the following quarternion:

Confusion in the Application of Quaternions

Hamilton tried to apply i, j, k as Vectors in a right handed System, which lead to much confusion in such applications. This confusion can be avoided if the the i, j, k are interpretated as bivectors in a left handed system.

In older books sometimes i, j. k can be found to name the three spatial unit vectors in a right handed system. Which is correct, if one does not interpret them as elements of a quaternion. Hamilton introduced vectors into the main stream of mathematics in this form. Gibbs developed the vector analysis to overcome the difficulties introduced by the misinterpretation of quaternions. On the other hand quaternions are an powerfull tool to perform rotations.

Biquaternions

Quaternions and Biquaternions are elements of the Form:

For quaternions   q₀, q₁, q₂, q₃ are real numbers.

For biquaternions q₀, q₁, q₂, q₃ are complex numbers.

Quaternions in Matrix Form

Quaternions as 2x2 matrices

The presentation of quaternions as 2x2 matrices with complex matrix elements looks as follows:

Quaternions as 4x4 Matrices

Replaching the elements of the 2x2 quaternion matrices by the following 2x2 matrices...

...will result in the following 4x4 matrices:

These matrices have the same properties as the quaternions:

i² = j² = k² = ijk = -I

These relations will result in the following matrix representation by 4x4 matrices:

The Presentation of the quaternions by 4x4 matrices is not unique. Exchanging the elements in the Kronecker product will give another matrix representation of the quaternions:

The matrix B can be interpretated as complex unit i of the complex numbers with i² = -1. Also (-i)² = -1.

Using -B gives another set of matrices:

Exchanging the elements of the Kronecker Produckt will give:

Base Matrices of the Quaternions

The quaternionen base elements represented as 4x4 matrices can generated by the Kronecker product of the basic 2x2 matrices I, U, H and B. The presentation of the quaternion base elements is not unique. There are several possibilities to implement quaternions by 4x4 matrices.

Example 1

Example 2

Example 3

Matrix Presentation of a Quaternion

q = aI + bi + cj + dk

The presentation of a quaternion in matrix form is not unique.

Example 1

Example 2

Pauli Matrices

The Pauli matrices contain the complex element i with the property i² = -1.

More on Pauli matrices as 2x2 matrices with complex elements can be found here:

2x2 Pauli Matrices

Pauli Matrices as 4x4 Matrices

Replaching the elements i, 1, 0 of the Pauli matrices by the following 2x2 matrices:

Will result into the following 4x4 matrices:

Matrix Representation of the Canonic Base Elements of the Geometric Algebra 𝔾³

Geometric algebra 𝔾³ by 4x4 matrices. The representation of the Geometric Algebra 𝔾³ by 4x4 matrices is not unique.

Example 1

Example 2

Kronecker Products

Kronecker products of the base matrices I, U, H and B.

Kronecker Product

The Cayley-Dickson Construction

A complex number z = a+bi can be represented as an ordered pair (a,b) of real numbers. The product of two complex numbers z₁ = (a,b) and z₂ = (c,d) is then defined as follows:

z₁z₂ = (a,b)(c,d)=(ac-bd, ad+cb)

The complex conjugate of a complex number z is defined as follows:

z = (a,b) = (a,-b)

Using the matrix representation of two complex numbers z₁, z₂ will give the following product:

The elements a,b,c,d are real numbers.

Using complex numbers instead of real numbers will result in the construction of the quaternions.

q = (z₁, z₂)

In this case the following, modified product has to be applied:

q₁q₂ = (z₁, z₂)(z₃, z₄) = (z₁z₃-z₂z₄, z₁z₄+z₃z₂) = q₃

This product will have the following matrix representation. In a first step the product of the two matrices with complex components is executed. Then all the required conjugations are executed.

The 2x2 matrices with complex components can be written as 4x4 matrices with real components, by using the substitution:

General Construction of Hypercomples Numbers

If a set of hypercomplex numbers is given the next set of hypercomplex numbers can be construted by using an order pair of the given hyper complex numbers (a,b) to construct the next higher set of hypercomplex numbers by applying the following rules:

(a,b)(c,d)= (ac-bd, ad+cb)

With the complex conjungate for hypercomplex numbers is defined as follows:

(a,b) = (a,-b)

Octonions

Sedenions

The next page is about Finite Groups.

Finite Groups