Wacker Art Functions I

Wacker Art

Further Functions I

Bild: "Edersee - Alte Brücke Scheid-Bringhausen"

Mathematical Functions

Functions

f(x) = e^-x²sin(x)	f(x) = e^-x²sin(2x)	f(x) = e^-x²sin(8x)
f(x) = e^-x²cos(x)	f(x) = e^-x²cos(2x)	f(x) = e^-x²cos(8x)
f(x) = sin(x)cos(x)
f(x) = sin(x)cos(2x)	f(x) = sin(x)cos(3x)	f(x) = sin(x)cos(12x)
f(x) = sin(2x)cos(x)	f(x) = sin(3x)cos(x)	f(x) = sin(12x)cos(x)

Bild: "Alte Baumstümpfe aus dem Edersee"

f(x) = sin(x)/x

f(x) = sin(4*x)/x

f(x) = sin(16*x)/x

f(x) = sin(1/x)

Bild: "Durchbruch Hammerberg"

Möbius Transformation

The Möbius transformation is defined by the following formular:

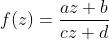
Möbius Transformation

with complex parameter a,b,c,d and one complex variable z.

If ad-bc = 0 and c≠0; the result of the transformation will be the constant value a/c.

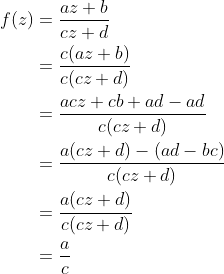
Möbius Transformation degenerated

This implies the following condition for the parameter a,b,c,d of the Möbius transformation:

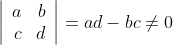
Möbius Condition

With this condition we have the Möbius transformation definded.

As next step we have some examples with Möbius transformations with real values. We will have the real valued parameter a,b,c,d and the real valued variable x.

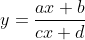
Möbius Transformation with Real Values

Asymtotic behavior for x → ∞ or x → -∞. For these limits the following constant y value will be approached:

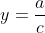
Asymptotic behavior of the Möbius transformation

If the denominator is zero the function has a pole (c ≠ 0); with the following x value:

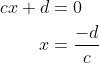
Pole of the Möbius transformation.

Values of the functions at x = 0.

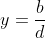
Value of the Möbius transformation at x=0.

x value for y=0

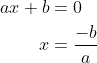
x value of the Möbius transformation at y=0.

Examples:

Parameter settings of the examples and the resulting values of the Möbius transformation.

a	b	c	d	Determinant	Asymptote y Value	Pole x Value	y=0 at x	y Value at x=0
1	1	1	-1	-2	1	1	-1	-1
1	1	-1	1	2	-1	1	-1	1
1	-1	1	1	2	1	-1	1	-1
-1	1	1	1	-2	-1	-1	1	1

Graphs of the Möbius transforms for real parameter

y = 1/(1+x²)

y = 2x/(1+x²)

y = (1-x²)/(1+x²)

y = 1/(1-x²)

y = x/(1-x²)

Bild: "Bootssteg"

y = x + 1/x

y = x² + 1/x²

Legendre Polynomials

7. März 2021 Version 2.0

Mathematical Functions

Functions

f(x) = e-x2sin(x)

f(x) = e-x2sin(2x)

f(x) = e-x2sin(8x)

f(x) = e-x2cos(x)

f(x) = e-x2cos(2x)

f(x) = e-x2cos(8x)

f(x) = sin(x)cos(x)

f(x) = sin(x)cos(2x)

f(x) = sin(x)cos(3x)

f(x) = sin(x)cos(12x)

f(x) = sin(2x)cos(x)

f(x) = sin(3x)cos(x)

f(x) = sin(12x)cos(x)

f(x) = sin(x)/x

f(x) = sin(4*x)/x

f(x) = sin(16*x)/x

f(x) = sin(1/x)

Möbius Transformation

Examples:

Graphs of the Möbius transforms for real parameter

try { var equation = new Array (); equation[0] = "&nbsp;&nbsp; y = "; equation[1] = frac("x+1", "x-1"); document.write(returnEquationTable(equation)); } catch (err) { document.write(errorMessage ("Moebius Example1", err)) }

try { var equation = new Array (); equation[0] = "&nbsp;&nbsp; y = "; equation[1] = frac("x+1", "-x+1"); document.write(returnEquationTable(equation)); } catch (err) { document.write(errorMessage ("Moebius Example2", err)) }

try { var equation = new Array (); equation[0] = "&nbsp;&nbsp; y = "; equation[1] = frac("x-1", "x+1"); document.write(returnEquationTable(equation)); } catch (err) { document.write(errorMessage ("Moebius Example3", err)) }

try { var equation = new Array (); equation[0] = "&nbsp;&nbsp; y = "; equation[1] = frac("-x+1", "x+1"); document.write(returnEquationTable(equation)); } catch (err) { document.write(errorMessage ("Moebius Example4", err)) }

y = 1/(1+x2)

y = 2x/(1+x2)

y = (1-x2)/(1+x2)

y = 1/(1-x2)

y = x/(1-x2)

y = x + 1/x

y = x2 + 1/x2

f(x) = e^-x²sin(x)

f(x) = e^-x²sin(2x)

f(x) = e^-x²sin(8x)

f(x) = e^-x²cos(x)

f(x) = e^-x²cos(2x)

f(x) = e^-x²cos(8x)

y = 1/(1+x²)

y = 2x/(1+x²)

y = (1-x²)/(1+x²)

y = 1/(1-x²)

y = x/(1-x²)

y = x² + 1/x²